
在 中,角
中,角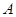 、
、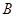 、
、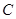 所对的边分别为
所对的边分别为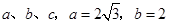 ,
,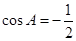 .
.
(1)求角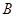 的大小;
的大小;
(2)若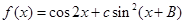 ,求函数
,求函数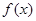 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
(1) ;(2)
;(2) ,
, .
.
解析试题分析:(1)解三角形问题先考虑运用正弦、余弦定理,此题先利用正弦定理可得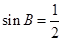 ,注意角A的余弦值为负值,即角A为钝角,在三角形ABC中,角B只能为锐角,所以
,注意角A的余弦值为负值,即角A为钝角,在三角形ABC中,角B只能为锐角,所以 ;(2)再利用正弦定理易得
;(2)再利用正弦定理易得 ,从而利用二倍角公式化简函数
,从而利用二倍角公式化简函数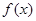 为一个角的三角函数式,易得函数
为一个角的三角函数式,易得函数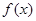 的周期,然后根据三角函数的性质求单调递增区间(此处注意一定要写成区间,并标明其中
的周期,然后根据三角函数的性质求单调递增区间(此处注意一定要写成区间,并标明其中 ).
).
试题解析:(1)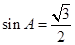 , 2分
, 2分
由 ,得
,得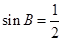 ,又A为钝角,故B为锐角,
,又A为钝角,故B为锐角, .(没指出B范围扣1分) 5分
.(没指出B范围扣1分) 5分
(2)  , 7分
, 7分
 , 9分
, 9分
所以,所求函数的最小正周期为 ,
,
由 ,得
,得 ,
,
所以所求函数的单调递增区间为 .(没写区间及指出K为整数扣1分) 12分
.(没写区间及指出K为整数扣1分) 12分
考点:1、正弦定理;2、二倍角公式;3、三角函数的单调区间.


科目:高中数学 来源: 题型:解答题
如图,甲船以每小时30 海里的速度向正北方向航行,
海里的速度向正北方向航行,
乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com