
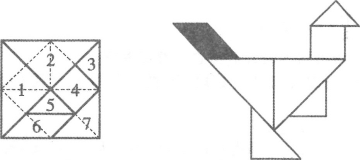
【题目】七巧板是一种古老的中国传统智力玩具,是由七块板组成的.而这七块板可拼成许多图形,例如:三角形、不规则多边形、各种人物、动物、建筑物等,清陆以湉《冷庐杂识》写道:近又有七巧图,其式五,其数七,其变化之式多至千余.在18世纪,七巧板流传到了国外,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.若用七巧板拼成一只雄鸡,在雄鸡平面图形上随机取一点,则恰好取自雄鸡鸡尾(阴影部分)的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】如图(1),在直角梯形![]() 中,
中,![]() 为
为![]() 的中点,四边形
的中点,四边形![]() 为正方形,将
为正方形,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达点
到达点![]() ,如图(2),
,如图(2),![]() 为
为![]() 的中点,且
的中点,且![]() ,点
,点![]() 为线段
为线段![]() 上的一点.
上的一点.

(1)证明:![]() ;
;
(2)当![]() 与
与![]() 夹角最小时,求平面
夹角最小时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点B(0,-2)和椭圆M:![]() .直线l:y=kx+1与椭圆M交于不同两点P,Q.
.直线l:y=kx+1与椭圆M交于不同两点P,Q.
(Ⅰ)求椭圆M的离心率;
(Ⅱ)若![]() ,求△PBQ的面积;
,求△PBQ的面积;
(Ⅲ)设直线PB与椭圆M的另一个交点为C,当C为PB中点时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】条件![]()
(1)条件![]() :复数
:复数![]() ,指明
,指明![]() 是
是![]() 的说明条件?若
的说明条件?若![]() 满足条件
满足条件![]() ,记
,记![]() ,求
,求![]()
(2)若上问中![]() ,记
,记![]() 时的
时的![]() 在平面直角坐标系的点
在平面直角坐标系的点![]() 存在过
存在过![]() 点的抛物线
点的抛物线![]() 顶点在原点,对称轴为坐标轴,求抛物线的解析式。
顶点在原点,对称轴为坐标轴,求抛物线的解析式。
(3)自(2)中![]() 点出发的一束光线经抛物线
点出发的一束光线经抛物线![]() 上一点
上一点![]() 反射后沿平行于抛物线
反射后沿平行于抛物线![]() 对称轴方向射出,求:
对称轴方向射出,求:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax-2|,不等式f(x)≤4的解集为{x|-2≤x≤6}.
(1)求实数a的值;
(2)设g(x)=f(x)+f(x+3),若存在x∈R,使g(x)-tx≤2成立,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com