
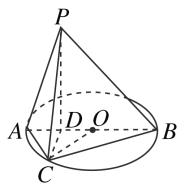
【题目】如图所示,已知AB为圆O的直径,且AB=4,点D为线段AB上一点,且![]() ,点C为圆O上一点,且
,点C为圆O上一点,且![]() .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.
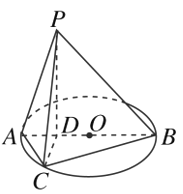
(1)求证:CD⊥平面PAB;
(2)求直线PC与平面PAB所成的角.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接CO,由题意可得△ACO为等边三角形,即得CD⊥AO,再由题意得PD⊥CD,即证得CD⊥平面PAB
(2)由(1)知∠CPD是直线PC与平面PAB所成的角,在三角形中结合各边长解三角形即可求出结果
(1)证明:连接CO,
由3AD=DB知,点D为AO的中点.
又因为AB为圆O的直径,所以AC⊥CB.
由![]() AC=BC知,∠CAB=60°,
AC=BC知,∠CAB=60°,
所以△ACO为等边三角形.故CD⊥AO.
因为点P在圆O所在平面上的正投影为点D,
所以PD⊥平面ABC,又CD平面ABC,所以PD⊥CD,
由PD平面PAB,AO平面PAB,且PD∩AO=D,
得CD⊥平面PAB.
(2)由(1)知∠CPD是直线PC与平面PAB所成的角,
又△AOC是边长为2的正三角形,所以CD=![]() .
.
在Rt△PCD中,PD=DB=3,CD=![]() ,
,
所以![]() ,∠CPD=30°,
,∠CPD=30°,
即直线PC与平面PAB所成的角为30°.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,如图1.已知
,如图1.已知![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() .
.


(1)求抛物线![]() 的方程;
的方程;
(2)若正方形![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 都在抛物线
都在抛物线![]() 上(如图2),求正方形
上(如图2),求正方形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABCD中,侧面PAD是正三角形,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.
(1)求证:PC⊥AD.
(2)在棱PB上是否存在一点Q,使得A,Q,M,D四点共面?若存在,指出点Q的位置并证明;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对于任意的
对于任意的![]()
![]() ,都有
,都有![]() ,当
,当![]() 时,
时,![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)当![]() 时,求函数
时,求函数![]() 的最大值和最小值;
的最大值和最小值;
(3)设函数![]() ,判断函数g(x) 最多有几个零点,并求出此时实数m的取值范围.
,判断函数g(x) 最多有几个零点,并求出此时实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点.

(1)求证:OM∥平面PAB;
(2)求证:平面PBD⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数![]() 的不足近似值和过剩近似值分别为
的不足近似值和过剩近似值分别为![]() 和
和![]()
![]() ,则
,则![]() 是
是![]() 的更为精确的近似值.
的更为精确的近似值.
我们知道![]() ,我国早在《周髀算经》中就有“周三径一”的古率记载,《隋书律历志》有如下记载:“南徐州从事史祖冲之更开密法,以圆径一亿为丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽,肭数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈肭二限之间。密率:圆径一百一十三,圆周三百五十五。约率,圆径七,周二十二”,这一记录指出了祖冲之关于圆周率的两大贡献:其一是求得圆周率
,我国早在《周髀算经》中就有“周三径一”的古率记载,《隋书律历志》有如下记载:“南徐州从事史祖冲之更开密法,以圆径一亿为丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽,肭数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈肭二限之间。密率:圆径一百一十三,圆周三百五十五。约率,圆径七,周二十二”,这一记录指出了祖冲之关于圆周率的两大贡献:其一是求得圆周率![]() ;其二是得到
;其二是得到![]() 的两个近似分数即:约率为22/7,密率为355/113,他算出的
的两个近似分数即:约率为22/7,密率为355/113,他算出的![]() 的8位可靠数字,不但在当时是最精密的圆周率,而且保持世界纪录一千多年,他对
的8位可靠数字,不但在当时是最精密的圆周率,而且保持世界纪录一千多年,他对![]() 的研究真可谓“运筹于帷幄之中,决胜于千年之外”,祖冲之是我国古代最有影响的数学家之一,莫斯科大学走廊里有其塑像,1959年10月,原苏联通过“月球3”号卫星首次拍下月球背面照片后,就以祖冲之命名一个环形山,其月面坐标是:东经148度,北纬17度.
的研究真可谓“运筹于帷幄之中,决胜于千年之外”,祖冲之是我国古代最有影响的数学家之一,莫斯科大学走廊里有其塑像,1959年10月,原苏联通过“月球3”号卫星首次拍下月球背面照片后,就以祖冲之命名一个环形山,其月面坐标是:东经148度,北纬17度.
纵横古今,关于![]() 值的研究,经历了古代试验法时期、几何法时期、分析法时期、蒲丰或然性试验方法时期、计算机时期,己知
值的研究,经历了古代试验法时期、几何法时期、分析法时期、蒲丰或然性试验方法时期、计算机时期,己知![]() ,试以上述
,试以上述![]() 的不足近似值
的不足近似值![]() 和过剩近似值
和过剩近似值![]() 为依据,那么使用两次“调日法”后可得
为依据,那么使用两次“调日法”后可得![]() 的近似分数为____________
的近似分数为____________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)
炼钢是一个氧化降碳的过程,由于钢水含碳量的多少直接影响冶炼时间的长短,因此必须掌握钢水含碳量和冶炼时间的关系.现已测得炉料熔化完毕时钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出钢的时间)的一组数据,如下表所示:

(1)据统计表明,![]() 之间具有线性相关关系,请用相关系数r加以说明(
之间具有线性相关关系,请用相关系数r加以说明(![]()
![]() ,则认为y与x有较强的线性相关关系,否则认为没有较强的线性相关关系,r精确到0.001);
,则认为y与x有较强的线性相关关系,否则认为没有较强的线性相关关系,r精确到0.001);
(2)建立y关于x的回归方程(回归系数的结果精确到0.01);
(3)根据(2)中的结论,预测钢水含碳量为160个0.01%的冶炼时间.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,
![]() ,相关系数
,相关系数
参考数据: ,
,
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com