Question

已知椭圆的焦点坐标为F1(－1,0)，F2(1,0)，过F2垂直于长轴的直线交椭圆于P，Q两点，且|PQ|＝3.

(1)求椭圆的方程；

(2)过F2的直线l与椭圆交于不同的两点M，N，则△F1MN的内切圆的面积是否存在最大值？若存在，求出这个最大值及此时的直线方程；若不存在，请说明理由．

 

Answer 1

（1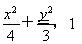）（2）l的方程为x＝1.

【解析】(1)设椭圆方程为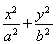＝1(a>b>0)，

由焦点坐标可得c＝1.由|PQ|＝3，可得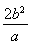＝3.

又a2－b2＝1，得a＝2，b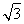＝.故椭圆方程为.

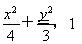(2)设M(x1，y1)，N(x2，y2)，不妨令y1>0，y2<0，

设△F1MN的内切圆的半径R，

则△F1MN的周长为4a＝8，S△F1MN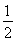＝ (|MN|＋|F1M|＋|F1N|)R＝4R，

因此要使△F1MN内切圆的面积最大，则R最大，此时S△F1MN也最大．

S△F1MN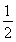＝|F1F2||y1－y2|＝y1－y2，

由题知，直线l的斜率不为零，可设直线l的方程为x＝my＋1，

由得(3m2＋4)y2＋6my－9＝0，

得y1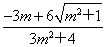＝，y2＝，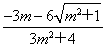

则S△F1MN＝y1－y2＝，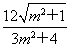

令t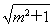＝，则t≥1，则S△F1MN＝.

令f(t)＝3t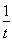＋，则f′(t)＝3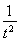－，当t≥1时，f′(t)>0，

所以f(t)在[1，＋∞)上单调递增，有f(t)≥f(1)＝4，S△F1MN≤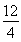＝3，

当t＝1，m＝0时，S△F1MN＝3，又S△F1MN＝4R，∴Rmax＝.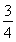

这时所求内切圆面积的最大值为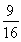π.

故△F1MN内切圆面积的最大值为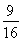π，且此时直线l的方程为x＝1.