练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在平面直角坐标系xOy中，以x轴正半轴为始边作锐角α，其终边与单位圆交于点A．以OA为始边作锐角β，其终边与单位圆交于点B，AB= ．
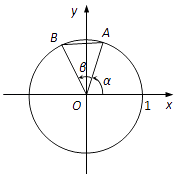
    （1）求cosβ的值；
    （2）若点A的横坐标为 ，求点B的坐标．

    【答案】
    （1）解：在△AOB中，由余弦定理得，AB2=OA2+OB2﹣2OAOBcos∠AOB，

    所以， = ，

    即


    （2）解：因为 ， ，∴ ．

    因为点A的横坐标为 ，由三角函数定义可得， ，

    因为α为锐角，所以 ．

    所以 ， ，

    即点 ．


    【解析】（1）由条件利用余弦定理，求得cosβ的值．（2）利用任意角的三角函数的定义，同角三角函数的基本关系，两角和差的正弦、余弦公式，求得点B的坐标．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】数列{an}满足a1+a2+a3+…an=2n﹣an（n∈N+）．数列{bn}满足bn= ，则{bn}中的最大项的值是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】水是地球上宝贵的资源，由于介个比较便宜在很多不缺水的城市居民经常无节制的使用水资源造成严重的资源浪费．某市政府为了提倡低碳环保的生活理念鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），[1，1.5），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图．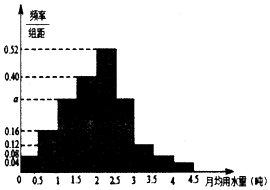
    （1）若全市居民中月均用水量不低于3吨的人数为3.6万，试估计全市有多少居民？并说明理由；
    （2）若该市政府拟采取分层抽样的方法在用水量吨数为[1，1.5）和[1.5，2）之间选取7户居民作为议价水费价格听证会的代表，并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖，设X为用水量吨数在[1，1.5）中的获奖的家庭数，Y为用水量吨数在[1.5，2）中的获奖家庭数，记随机变量Z=|X﹣Y|，求Z的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响，随机选取100名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案：电脑模拟驾驶，以某速度匀速行驶，记录下驾驶员的“停车距离”（驾驶员从看到意外情况到车子停下所需的距离），无酒状态与酒后状态下的实验数据分别列于表1和表2.

    表1：

    停车距离（米）

    频数

    26

    40

    24

    8

    2

    表2：

    平均每毫升血液酒精含量（毫克）

    10

    30

    50

    70

    90

    平均停车距离（米）

    30

    50

    60

    70

    90

    请根据表1，表2回答以下问题.

    （1）根据表1估计驾驶员无酒状态下停车距离的平均数；

    （2）根据最小二乘法，由表2的数据计算关于的回归方程.

    （3）该测试团队认为：驾驶员酒后驾车的“平均停车距离”大于（1）中无酒状态下的停车距离平均数的3倍，则认定驾驶员是“醉驾”.请根据（2）中的回归方程，预测当每毫升血液酒精含量大于多少毫克时为“醉驾”？参考公式：

    ，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为菱形，平面底面，且，，，为的中点.

    （1）证明：.

    （2）求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】高一某班级在学校数学嘉年华活动中推出了一款数学游戏，受到大家的一致追捧.游戏规则如下：游戏参与者连续抛掷一颗质地均匀的骰子，记第i次得到的点数为，若存在正整数n，使得，则称为游戏参与者的幸运数字。

    （I）求游戏参与者的幸运数字为1的概率；

    （Ⅱ）求游戏参与者的幸运数字为2的概率，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中正确的是（ ）

    A. 有两个面平行，其余各面都是四边形的几何体叫棱柱

    B. 有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱

    C. 用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台

    D. 有两个面平行，其余各面都是平行四边形的几何体叫棱柱

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的首项，其前项和为，对于任意正整数，，都有.

    （Ⅰ）求数列的通项公式；

    （Ⅱ）设数列满足，且.

    ①求证数列为常数列.

    ②求数列的前项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若以直角坐标系xOy的O为极点，Ox为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程是ρ= ．
    （1）将曲线C的极坐标方程化为直角坐标方程，并指出曲线是什么曲线；
    （2）若直线l的参数方程为 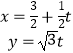（t为参数）当直线l与曲线C相交于A，B两点，求| |

    查看答案和解析>>

    同步练习册答案