
 .
.
 ,知∠HAB=30°,在△ABP中用正弦定理可得BP=
,知∠HAB=30°,在△ABP中用正弦定理可得BP= .
.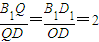 .
. (1)线段A1B上不存在一点P,使得A1B⊥平面PAC.
(1)线段A1B上不存在一点P,使得A1B⊥平面PAC. ,即
,即 ,
, ,
,
 =
= .
. …(10分)
…(10分) …(14分).
…(14分).

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
 如图,已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB以及B1C的中点处各有一个小孔E、G,在B1处有一个小孔,若此容器可以任意放置,则该容器可装水的最大容积为
如图,已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB以及B1C的中点处各有一个小孔E、G,在B1处有一个小孔,若此容器可以任意放置,则该容器可装水的最大容积为| 11 |
| 12 |
| 11 |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知棱长为1的正方体ABCD-A1B1C1D1.
如图,已知棱长为1的正方体ABCD-A1B1C1D1.| B1Q | QD |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知棱长为1的正方体ABCD-A1B1C1D1中,E是A1B1的中点,则直线AE与平面ABC1D1所成的角的正弦值是( )
如图,已知棱长为1的正方体ABCD-A1B1C1D1中,E是A1B1的中点,则直线AE与平面ABC1D1所成的角的正弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源:江苏省泰兴中学2007届高三数学二模适应性练习 题型:044
如图,已知棱长为1的正方体ABCD-A1B1C1D1.

(1)线段A1B上是否存在一点P,使得A1B⊥平面PAC?若存在,确定P点的位置,若不存在,说明理由;
(2)点P在A1B上,若二面角C―AP―B的大小是arctan2,求BP的长;
(3)Q点在对角线B1D,使得A1B∥平面QAC,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com