
【题目】已知直线![]() 、
、![]() 与曲线
与曲线![]() 分别相交于点
分别相交于点![]() 、
、![]() 和
和![]() 、
、![]() ,我们将四边形
,我们将四边形![]() 称为曲线
称为曲线![]() 的内接四边形.
的内接四边形.
(1)若直线![]() 和
和![]() 将单位圆
将单位圆![]() 分成长度相等的四段弧,求
分成长度相等的四段弧,求![]() 的值;
的值;
(2)若直线![]() ,
,![]() 与圆
与圆![]() 分别交于点
分别交于点![]() 、
、![]() 和
和![]() 、
、![]() ,求证:四边形
,求证:四边形![]() 为正方形;
为正方形;
(3)求证:椭圆![]() 的内接正方形有且只有一个,并求该内接正方形的面积.
的内接正方形有且只有一个,并求该内接正方形的面积.
【答案】(1)![]() (2)证明见解析 (3)证明见解析
(2)证明见解析 (3)证明见解析
【解析】
(1)根据直线分圆分成长度相等的四段弧,得到![]() ,利用点到直线的距离公式进行求解即可.
,利用点到直线的距离公式进行求解即可.
(2)根据直线与圆相交的位置关系,利用消元法转化为一元二次方程,根据根与系数之间的关系进行证明即可;
(3)根据椭圆内接正方形的关系,转化为一元二次方程,根据根与系数之间的关系进行证明即可.
解:(1)由于直线![]() 和
和![]() 将单位圆
将单位圆![]() 分成长度相等的四段弧,
分成长度相等的四段弧,
所以![]() ,
,
在等腰直角![]() 中,圆心
中,圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,∴
,∴![]() ,
,
同理![]() ,∴
,∴![]() ;
;
(2)由题知,直线![]() ,
,![]() 关于原点对称,因为圆
关于原点对称,因为圆![]() 的圆心为原点
的圆心为原点![]() ,
,
所以![]() ,故四边形
,故四边形![]() 为平行四边形.易知,
为平行四边形.易知,![]() 点在对角线
点在对角线![]() ,
,![]() 上.
上.
联立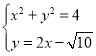 解得
解得![]() ,由
,由![]() ,
,![]() 得
得
![]()
![]() ,
,
所以![]() ,
,
于是![]() ,因为
,因为![]() ,所以四边形
,所以四边形![]() ABCD为正方形.
ABCD为正方形.
(3)证明:假设椭圆![]() 存在内接正方形,其四个顶点为
存在内接正方形,其四个顶点为![]() ,
,![]() ,
,![]() ,
,![]() .
.
当直线![]() 的斜率不存在时,设直线
的斜率不存在时,设直线![]() 、
、![]() 的方程为
的方程为![]() ,
,![]() ,因为
,因为![]() ,
,![]() ,
,![]() ,
,![]() 在椭圆上,
在椭圆上,
所以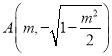 ,
,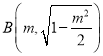 ,
,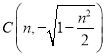 ,
,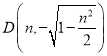 .
.
由四边形![]() 为正方形,易知,
为正方形,易知,![]() ,
,![]() ,直线
,直线![]() 、
、![]() 的方程为
的方程为![]() ,
,![]() ,
,
正方形![]() 的面积
的面积![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 、
、![]() 的方程分别为
的方程分别为![]() ,
,![]() ,
,
显然![]() .设
.设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立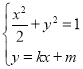 得
得![]() ,所以
,所以![]() ,
,![]()
代人![]() ,得
,得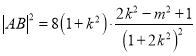 ,
,
同理可得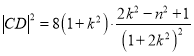 ,
,
因为![]() 为正方形,所以
为正方形,所以![]() 解得
解得![]()
因为![]() ,所以
,所以![]() ,
,
因此,直线![]() 与直线
与直线![]() 关于原点
关于原点![]() 对称,
对称,
所以原点![]() 为正方形的中心(由
为正方形的中心(由![]() 知
知![]() ,四边形
,四边形![]() 为平行四边形
为平行四边形
由![]() 为正方形知
为正方形知![]() ,
,
即![]()
代入得![]() ,解得
,解得![]() (注:此时四边形
(注:此时四边形![]() 为菱形)
为菱形)
由![]() 为正方形知
为正方形知![]() ,
,
因为直线![]() 与直线
与直线![]() 的距离为
的距离为![]() ,
,![]() ,故
,故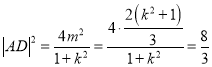
但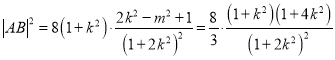 ,
,
由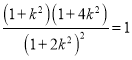 得
得![]() ,
,
∴![]() 即
即![]() ,与
,与![]() 矛盾.
矛盾.
所以![]() ,这与
,这与![]() 矛盾.
矛盾.
即当直线![]() 的斜率
的斜率![]() 存在时,椭圆内不存在正方形.
存在时,椭圆内不存在正方形.
综上所述,椭圆![]() 的内接正方形有且只有一个,且其面积为
的内接正方形有且只有一个,且其面积为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】王老师是高三的班主任,为了在寒假更好的督促班上的学生完成学习作业,王老师特地组建了一个QQ群,群的成员由学生、家长、老师共同组成.已知该QQ群中男学生人数多于女学生人数,女学生人数多于家长人数,家长人数多于教师人数,教师人数的两倍多于男学生人数.则该QQ群人数的最小值为( )
A.20B.22C.26D.28
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,
,![]() 与短轴的一个端点构成一个等边三角形,且直线
与短轴的一个端点构成一个等边三角形,且直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)已知过椭圆![]() 的左顶点
的左顶点![]() 的两条直线
的两条直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(3)在(2)的条件下求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某健身馆在2019年7、8两月推出优惠项目吸引了一批客户.为预估2020年7、8两月客户投入的健身消费金额,健身馆随机抽样统计了2019年7、8两月100名客户的消费金额,分组如下:![]() ,
,![]() ,
,![]() ,…,
,…,![]() (单位:元),得到如图所示的频率分布直方图:
(单位:元),得到如图所示的频率分布直方图:
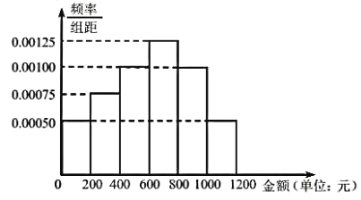
(1)请用抽样的数据预估2020年7、8两月健身客户人均消费的金额(同一组中的数据用该组区间的中点值作代表);
(2)若把2019年7、8两月健身消费金额不低于800元的客户,称为“健身达人”,经数据处理,现在列联表中得到一定的相关数据,请补全空格处的数据,并根据列联表判断是否有![]() 的把握认为“健身达人”与性别有关?
的把握认为“健身达人”与性别有关?
健身达人 | 非健身达人 | 总计 | |
男 | 10 | ||
女 | 30 | ||
总计 |
(3)为吸引顾客,在健身项目之外,该健身馆特别推出健身配套营养品的销售,现有两种促销方案.
方案一:每满800元可立减100元;
方案二:金额超过800元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
若某人打算购买1000元的营养品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
附:
| 0.100 | 0.050 | 0.010 | 0.005 | |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题:“若![]() ,
,![]() 为异面直线,平面
为异面直线,平面![]() 过直线
过直线![]() 且与直线
且与直线![]() 平行,则直线
平行,则直线![]() 与平面
与平面![]() 的距离等于异面直线
的距离等于异面直线![]() ,
,![]() 之间的距离”为真命题.根据上述命题,若
之间的距离”为真命题.根据上述命题,若![]() ,
,![]() 为异面直线,且它们之间的距离为
为异面直线,且它们之间的距离为![]() ,则空间中与
,则空间中与![]() ,
,![]() 均异面且距离也均为
均异面且距离也均为![]() 的直线
的直线![]() 的条数为( )
的条数为( )
A.0条B.1条C.多于1条,但为有限条D.无数多条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水稻就是耐盐碱水稻,是一种介于野生稻和栽培稻之间的普遍生长在海边滩涂地区的水稻,具有抗旱抗涝、抗病虫害、抗倒伏抗盐碱等特点.近年来,我国的海水稻研究取得了阶段性成果,目前已开展了全国大范围试种.某农业科学研究所分别抽取了试验田中的海水稻以及对照田中的普通水稻各![]() 株,测量了它们的根系深度(单位:
株,测量了它们的根系深度(单位:![]() ),得到了如下的茎叶图,其中两竖线之间表示根系深度的十位数,两边分别是海水稻和普通水稻根系深度的个位数,则下列结论中不正确的是( )
),得到了如下的茎叶图,其中两竖线之间表示根系深度的十位数,两边分别是海水稻和普通水稻根系深度的个位数,则下列结论中不正确的是( )
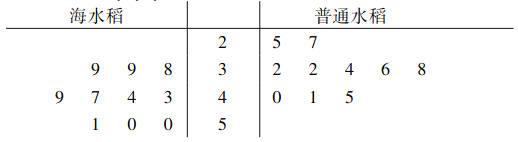
A.海水稻根系深度的中位数是![]()
B.普通水稻根系深度的众数是![]()
C.海水稻根系深度的平均数大于普通水稻根系深度的平均数
D.普通水稻根系深度的方差小于海水稻根系深度的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 和
和![]() 是双曲线
是双曲线![]() 上的两点,线段
上的两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 不经过坐标原点
不经过坐标原点![]() .
.
(1)若直线![]() 和直线
和直线![]() 的斜率都存在且分别为
的斜率都存在且分别为![]() 和
和![]() ,求证:
,求证:![]() ;
;
(2)若双曲线的焦点分别为![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求由四点
,求由四点![]() 、
、![]() 、
、![]() 、
、![]() 所围成四边形
所围成四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com