
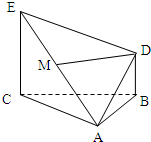
 如图所示,△ABC为正三角形,EC⊥底面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,
如图所示,△ABC为正三角形,EC⊥底面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,
| ||
. |
| ||
. |


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
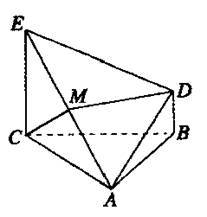
(08年聊城市三模)(12分) 如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.
(I)证明:DM∥平面ABC;
(II)证明:CM⊥DE;
(III)求平面ADE与平面ABC所成的二面角的大小(只考虑锐角情况).
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,△ABC为直角三角形,∠C=90°,若![]() =(0,-4),M在
=(0,-4),M在![]() 轴上,且AM=
轴上,且AM=![]() ,点C在
,点C在![]() 轴上移动.
轴上移动.
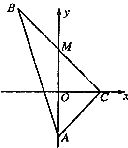
(Ⅰ)求点B的轨迹E的方程;
(Ⅱ)过点F(0,![]() )的直线
)的直线![]() 与曲线E交于P、Q两点,设N(0,
与曲线E交于P、Q两点,设N(0,![]() )(
)(![]() <0),
<0),![]() 与
与![]() 的夹角为
的夹角为![]() ,若
,若![]() ≤
≤![]() 等恒成立,求
等恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)设以点N为圆心,以![]() 半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求
半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:

求证:(1)DE=DA;
(2)平面MBD⊥平面ECA;
(3)平面DEA⊥平面ECA.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE,且CE=AC=2BD,M是AE的中点.
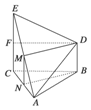
(1)求证:DE=DA;
(2)求证:平面BDM⊥平面ECA;
(3)求证:平面DEA⊥平面ECA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com