
 已知数列{an},观察程序框图,若k=5时,分别有S=25.
已知数列{an},观察程序框图,若k=5时,分别有S=25.分析 (1)由框图可知{an}为等差数列,且公差为2,由题意得当k=5时,有5a1+25-5=25,由此求出首项,由此能求出数列{an}的通项.
(2)由已知各bn=2an=22n-1,由此能{bn}的前n项和Tn的值.
解答 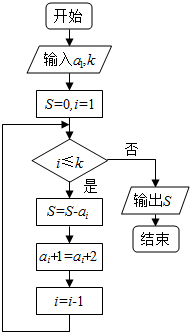 解:(1)由框图可知{an}为等差数列,且公差为2,Sn为{an}前n项和,
解:(1)由框图可知{an}为等差数列,且公差为2,Sn为{an}前n项和,
Sn=na1+$\frac{n(n-1)d}{2}$=na1+n2-n
由题意得当k=5时,有S=25,
所以5a1+25-5=25,
解得a1=1,
所以an=a1+(n-1)d=2n-1.
(2)由(1)可得:bn=2an=22n-1
∴b1+b2+…+bm
=21+23+…+22m-1
=$\frac{2(1-{4}^{m})}{1-4}$=$\frac{2}{3}$(4m-1).
点评 本题考查数列的通项公式和前n项和的求法,是中档题,解题时要注意等差数列、等比数列的性质和程序框图的性质的合理运用.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | tanα | B. | tan2α | C. | $\frac{1}{3}$tan2α | D. | cotα |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com