分析:(Ⅰ)根据抛物线方程设出P,Q的坐标,把P,Q分别代入抛物线方程进行求导,可求得直线TP,TQ的斜率,进而利用两点表示出两直线的斜率,建立等式整理后可推断出x1,x2为方程x2-2tx-1=0的两根,利用韦达定理可表示出x1+x2和x1x2,进而利用点斜式表示出直线PQ的方程,整理后把x1+x2和x1x2的表达式代入,求得y=2tx+2,进而可推断出直线PQ恒过定点(0,2)
(Ⅱ)设出点M的坐标,进而利用三角形面积公式表示出△OTM的面积,根据直线PQ恒过定点(0,2),设直线PQ方程,代入抛物线方程,整理后,利用韦达定理求得(x1+x2)=Kx1x2=-1.利用二次函数的性质可k的值确定y0的最小值,进而确定S△OTM|OT|的最小值.
解答:解:(Ⅰ)设P(x
1,x
12+1),Q(x
2,x
22+1)
把P代入抛物线方程进行求导得y'=2x
1,即PT的斜率为2x
1,
∴
=2x
1,整理得x
12-2tx
1-1=0;同理可得x
22-2tx
2-1=0
∴x
1,x2为方程x
2-2tx-1=0的两根
∴x
1+x
2=2t,x
1x
2=-1
直线PQ的方程:y-(x
12+1)=
(x-x
1)
整理得:y=(x
1+x
2)x-x
1x
2+1;即y=2tx+2
∴直线PQ恒过定点(0,2)
(Ⅱ)设点M坐标为(x
0,y
0),则s
△OTM:|OT|=
(y0•|t|):|t|=,
由(Ⅰ)直线PQ过定点N(0,2),
设直线PQ方程为y=kx+2代入y=x
2+1整理得x
2-kx-1=0,
设p(x
1,y
1)Q(x
1,y
2),则(x
1+x
2)=Kx
1x
2=-1,y
0=k
0+2=
k•+2=+2≥2,
当k=0时,y
0最小值为:2,
所以s
△OTM|OT|最小值为:1.
点评:本题主要考查了抛物线的应用和直线与抛物线的关系.注重了学生分析推理和基本的计算能力的考查.

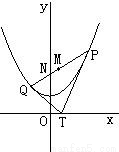
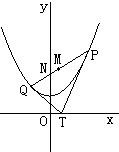 过x轴上的动点T(t,0),引抛物线y=x2+1两条切线TP,TQ,P,Q为切点.
过x轴上的动点T(t,0),引抛物线y=x2+1两条切线TP,TQ,P,Q为切点.

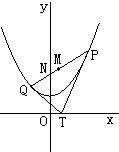 过x轴上的动点T(t,0),引抛物线y=x2+1两条切线TP,TQ,P,Q为切点.
过x轴上的动点T(t,0),引抛物线y=x2+1两条切线TP,TQ,P,Q为切点.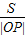 的最小值.
的最小值.