
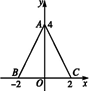
如图所示,△ABC三个顶点坐标为A(0,4),B(-2,0),C(2,0),求△ABC内任一点(x,y)所满足的条件.
|
解:直线AB:2x-y+4=0, 直线AC:2x+y-4=0, 直线BC:y=0. 将(0,0)代入2x-y+4得4>0成立, ∴原点在不等式2x-y+4>0表示的区域内. 将(0,0)代入2x+y-4得-4<0成立,∴原点在不等式2x+y-4<0表示的区域内. 显然△ABC位于y=0的上方,∴满足的不等式为y>0. △ABC内任一点(x,y)所满足的条件为 思路解析:先写出AB、AC、BC三条直线的方程,再用特殊点法检验△ABC内的区域可用哪些不等式表示. |
|
绿色通道:此类题目求解的一般步骤是: (1)导出边界直线; (2)分别代点检验公共区域满足的不等式; (3)写出不等式组. |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
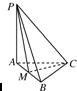 19、如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.
19、如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.查看答案和解析>>
科目:高中数学 来源: 题型:
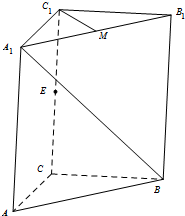 如图所示,直三棱柱ABC-A1B1C1中,CA=CB,∠BCA=90°,E、M分别是CC1、A1B1的中点.
如图所示,直三棱柱ABC-A1B1C1中,CA=CB,∠BCA=90°,E、M分别是CC1、A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 电子跳蚤游戏盘是如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处,BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳回到BC边的P3处,且BP3=BP2,…,跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2007与P2010间的距离为
电子跳蚤游戏盘是如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处,BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳回到BC边的P3处,且BP3=BP2,…,跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2007与P2010间的距离为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com