
分析 当x>1时f(x)=ax单调递增,当x≤1时f(x)=(2-$\frac{a}{2}$)x+2单调递增,且(2-$\frac{a}{2}$)×1+2≤a1,由此能求出实数a取值范围.
解答 解:∵f(x)=$\left\{\begin{array}{l}{{a}^{x},x>1}\\{(2-\frac{a}{2})x+2,x≤1}\end{array}\right.$是(-∞,+∞)上的增函数,
∴当x>1时f(x)=ax单调递增,则a>1①;
当x≤1时f(x)=(2-$\frac{a}{2}$)x+2单调递增,
则2-$\frac{a}{2}$>0,解得a<4,②;
且(2-$\frac{a}{2}$)×1+2≤a1,解得a≥$\frac{8}{3}$,③.
综合①②③,得实数a取值范围是[$\frac{8}{3}$,4).
故答案为:[$\frac{8}{3}$,4].
点评 本题考查实数值的取值范围的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 “健步走”是一种方便而又有效的锻炼方式,李老师每天坚持“健步走”,并用计步器进行统计.他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如表:
“健步走”是一种方便而又有效的锻炼方式,李老师每天坚持“健步走”,并用计步器进行统计.他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如表:| 步数(千卡) | 16 | 17 | 18 | 19 |
| 消耗能量(卡路里) | 400 | 440 | 480 | 520 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
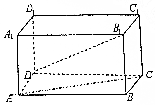 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com