练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知为的三个内角，且其对边分别为，若．

    （1）求角的值；

    （2）若，求的面积．

    【答案】（1）；（2）．

    【解析】分析：（1）先由正弦定理得,再根据特殊角三角函数值得角的值；（2）根据余弦定理得bc=4，再根据三角形面积公式得结果.

    详解：（1）∵acosC+ccosA=-2bcosA，

    由正弦定理可得：sinAcosC+sinCcosA=-2sinBcosA，

    化为：sin（A+C）=sinB=2sinBcosA，sinB≠0，

    可得cosA=，A∈（0，），∴A=；

    （2）由，b+c=4，结合余弦定理，得a2=b2+c2-2bccosA，

    ∴12=（b+c）2-2bc-2bccos，即有12=16-bc，化为bc=4．

    故△ABC的面积为S=bcsinA=×4×sin=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】求由直线x＝1、x＝2、y＝0及曲线围成的图形的面积S.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为a，E、F、G、H分别为AB、BC、CD、DA的中点．若沿EF、FG、GH、HE将四角折起，试问能折成一个四棱锥吗？为什么？你从中能得到什么结论？对于圆锥有什么类似的结论？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF＝，则下列结论中错误的是

    A．AC⊥BE B．EF∥平面ABCD

    C．三棱锥A-BEF的体积为定值 D．异面直线AE，BF所成的角为定值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】己知函数.

    （Ⅰ）当时，解关于x的不等式；

    （Ⅱ）若不等式的解集为D，且，求m的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四面体中，已知⊥平面， ， ， 为的中点．

    （1）求证： ；

    （2）若为的中点，点在直线上，且，

    求证：直线//平面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C经过两点A（3，3），B（4，2），且圆心C在直线上。

    （Ⅰ）求圆C的方程；

    （Ⅱ）直线过点D（2，4），且与圆C相切，求直线的方程。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某公园摩天轮的半径为，圆心距地面的高度为，摩天轮做匀速转动，每转一圈，摩天轮上的点的起始位置在最低点处.

    （1）已知在时刻时距离地面的高度，（其中），求时距离地面的高度；

    （2）当离地面以上时，可以看到公园的全貌，求转一圈中有多少时间可以看到公园的全貌？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

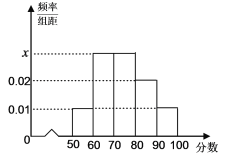
    【题目】2018年高考特别强调了要增加对数学文化的考查，为此某校高三年级特命制了一套与数学文化有关的专题训练卷（文、理科试卷满分均为100分），并对整个高三年级的学生进行了测试，现从这些学生中随机抽取了50名学生的成绩，按照成绩为，，…，分成了5组，制成了如图所示的频率分布直方图（假定每名学生的成绩均不低于50分）.

    （Ⅰ）求频率分布直方图中的的值，并估计所抽取的50名学生成绩的中位数（用分数表示）；

    （Ⅱ）若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人，再从这6人中随机抽取2人参加这次考试的考后分析会，试求组中至少有1人被抽到的概率.

    查看答案和解析>>

    同步练习册答案