
| A. | $\frac{\sqrt{2}+\sqrt{10}}{6}$ | B. | $\frac{2\sqrt{2}+\sqrt{10}}{6}$ | C. | $\frac{\sqrt{2}-\sqrt{10}}{6}$ | D. | $\frac{2\sqrt{2}-\sqrt{10}}{6}$ |
分析 可先由同角三角函数的基本关系求出θ的正弦,然后由余弦的和角公式求出的值即可得到答案
解答 解:cosθ=$\frac{2}{3}$,θ为第四象限角,得sinθ=-$\sqrt{1-\frac{4}{9}}$=-$\frac{\sqrt{5}}{3}$,
∴cos(θ+$\frac{π}{4}$)=cosθcos$\frac{π}{4}$-sinθsin$\frac{π}{4}$=$\frac{2}{3}$×$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{5}}{3}$×$\frac{\sqrt{2}}{2}$=$\frac{2\sqrt{2}+\sqrt{10}}{6}$.
故选:B
点评 本题考点是三角函数的恒等变换及化简求值,考查了同角三角函数的基本关系,余弦的和角公式,解题的关键是熟练掌握三角函数的公式,利用公式求值,三角函数公式较多,变形灵活,做题时要注意总结规律,找到最佳的变形方法进行求值.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $2\sqrt{3}$ | C. | $3\sqrt{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费x/万元 | 4 | 2 | 3 | 5 |
| 销售额y/万元 | 49 | 26 | 39 | 54 |
| A. | 63.6万元 | B. | 65.5万元 | C. | 67.7万元 | D. | 72.0万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4π}$ | B. | $\frac{1}{2π}$ | C. | $\frac{1}{π}$ | D. | $\frac{2}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份x | 2012 | 2013 | 2014 | 2015 | 2016 |
| 网上交易额y(亿元) | 5 | 6 | 7 | 8 | 10 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| z | 0 | 1 | 2 | 3 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
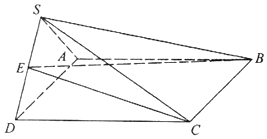 如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,平面SAD⊥平面SCD,$SA=SD=2\sqrt{2}$.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,平面SAD⊥平面SCD,$SA=SD=2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com