
【题目】如图,在直三棱柱ABC-A1B1C1中,∠ABC=![]() ,D是棱AC的中点,且AB=BC=BB1=2.
,D是棱AC的中点,且AB=BC=BB1=2.
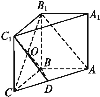
(1)求证:AB1∥平面BC1D;
(2)求异面直线AB1与BC1所成的角.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接B1C交BC1于点O,连接OD.利用三角形中位线说明OD∥AB1即得证。
(2)建立空间坐标系,求出![]() =(0,-2,2),
=(0,-2,2),![]() =(2,0,2).代入夹角计算公式即可。
=(2,0,2).代入夹角计算公式即可。
(1)证明如图,连接B1C交BC1于点O,连接OD.
因为O为B1C的中点,D为AC的中点,所以OD∥AB1.
因为AB1平面BC1D,OD平面BC1D,
所以AB1∥平面BC1D.
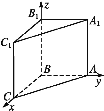
(2)解建立如图所示的空间直角坐标系Bxyz,
则B(0,0,0),A(0,2,0),C1(2,0,2),B1(0,0,2),
因此![]() =(0,-2,2),
=(0,-2,2),![]() =(2,0,2).
=(2,0,2).
所以cos<![]() >=
>=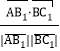 =
=![]() ,
,
设异面直线AB1与BC1所成的角为θ,则cos θ=![]() ,由于θ∈
,由于θ∈![]() ,故θ=
,故θ=![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,动圆经过点M(a﹣2,0),N(a+2,0),P(0,﹣2),其中a∈R.
(1)求动圆圆心的轨迹E的方程;
(2)过点P作直线l交轨迹E于不同的两点A、B,直线OA与直线OB分别交直线y=2于两点C、D,记△ACD与△BCD的面积分别为S1 , S2 . 求S1+S2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为 ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)设X表示一辆车从甲地到乙地遇到红灯的个数,求随机变量X的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1边长为1,下底面ABCD边长为2,侧棱与底面所成的角为60°,则异面直线AD1与B1C所成角的余弦值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
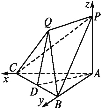
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,△ABC是直角三角形,且PA=AB=AC.又平面QBC垂直于底面ABC.
(1)求证:PA∥平面QBC;
(2)若PQ⊥平面QBC,求锐二面角Q-PB-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE=_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划2011年在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲、乙两个电视台为该公司每分钟所做的广告,能给公司带来的收益分别为0.3 万元和0.2万元.问:该公司如何分配在甲、乙两个电视台的广告时间,才能使公司收益最大,最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.

(1)求证:MN∥BC;
(2)若M,N分别为PB,PC的中点,
①求证:PB⊥DN;
②求二面角P-DN-A的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com