
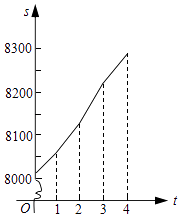
【题目】一辆汽车在某段路程中的行驶速率与时间的关系如图所示. 
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车在行驶该段路程前里程表的读数是8018km,试求汽车在行驶这段路程时里程表读数s(km)与时间t (h)的函数解析式,并作出相应的图象.
【答案】
(1)解:阴影部分的面积为:
50+70+90+60=270,
表示汽车在4小时内行驶的路程为270 km
(2)解:∵这辆汽车在行驶该段路程前里程表的读数是8018km,
汽车在行驶这段路程时里程表读数s(km)与时间t (h)的函数解析式为:
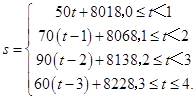
图象如下图:
【解析】(1)由频率分布图能求出阴影部分的面积,表示汽车在4小时内行驶的路程.(2)由这辆汽车在行驶该段路程前里程表的读数是8018km,结合频率分布直方图能求出汽车在行驶这段路程时里程表读数s(km)与时间t (h)的函数解析式,并能作出图象.
【考点精析】通过灵活运用频率分布直方图,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+φ1),g(x)=cos(4x+φ2),|φ1|≤ ![]() ,|φ2|≤
,|φ2|≤ ![]() . 命题①:若直线x=φ是函数f(x)和g(x)的对称轴,则直线x=
. 命题①:若直线x=φ是函数f(x)和g(x)的对称轴,则直线x= ![]() kπ+φ(k∈Z)是函数g(x)的对称轴;
kπ+φ(k∈Z)是函数g(x)的对称轴;
命题②:若点P(φ,0)是函数f(x)和g(x)的对称中心,则点Q( ![]() +φ,0)(k∈Z)是函数f(x)的中心对称.( )
+φ,0)(k∈Z)是函数f(x)的中心对称.( )
A.命题①②都正确
B.命题①②都不正确
C.命题①正确,命题②不正确
D.命题①不正确,命题②正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣x2 , 若存在实数a,b,使f(x)在[a,b]上的值域为[ ![]() ,
, ![]() ],则ab= .
],则ab= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义min{a,b}= ![]() ,若函数f(x)=min{x2﹣3x+3,﹣|x﹣3|+3},且f(x)在区间[m,n]上的值域为[
,若函数f(x)=min{x2﹣3x+3,﹣|x﹣3|+3},且f(x)在区间[m,n]上的值域为[ ![]() ,
, ![]() ],则区间[m,n]长度的最大值为( )
],则区间[m,n]长度的最大值为( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知偶函数f(x)和奇函数g(x)的定义域都是(﹣4,4),且在(﹣4,0]上的图象如图所示,则关于x的不等式f(x)g(x)<0的解集是 . 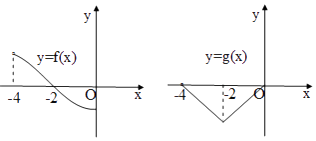
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组中的函数f(x),g(x)表示同一函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)=x+1,g(x)= ![]()
C.f(x)=|x|,g(x)= ![]()
D.f(x)=log22x , g(x)=2log2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ< ![]() ),L为等腰梯形ABCD的周长.
),L为等腰梯形ABCD的周长. 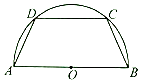
(1)求周长L与θ的函数解析式;
(2)试问周长L是否存在最大值?若存在,请求出最大值,并指出此时θ的大小;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为角A,B,C所对的边,角C是钝角,且sinB= ![]() .
.
(1)求角C的值;
(2)若b=2,△ABC的面积为 ![]() ,求c的值.
,求c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com