
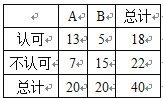
ЁОЬтФПЁПЯждкЃЌКмЖрШЫЖМЯВЛЖЦяЁАЙВЯэЕЅГЕЁБЃЌЕЋвВгаКмЖрЪаУёВЂВЛШЯПЩЃЎЮЊСЫЕїВщШЫУЧЖдетжжНЛЭЈЗНЪНЕФШЯПЩЖШЃЌФГЭЌбЇДгНЛЭЈгЕЖТВЛбЯжиЕФAГЧЪаКЭНЛЭЈгЕЖТбЯжиЕФBГЧЪаЗжБ№ЫцЛњЕїВщСЫ20УћЪаУёЃЌЕУЕНСЫвЛИіЪаУёЪЧЗёШЯПЩЕФбљБОЃЌОпЬхЪ§ОнШчЯТ![]() СаСЊБэЃК
СаСЊБэЃК
ИНЃК![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ

ИљОнБэжаЕФЪ§ОнЃЌЯТСаЫЕЗЈжаЃЌе§ШЗЕФЪЧЃЈ ЃЉ
A. УЛга95% вдЩЯЕФАбЮеШЯЮЊЁАЪЧЗёШЯПЩгыГЧЪаЕФгЕЖТЧщПігаЙиЁБ
B. га99% вдЩЯЕФАбЮеШЯЮЊЁАЪЧЗёШЯПЩгыГЧЪаЕФгЕЖТЧщПігаЙиЁБ
C. ПЩвддкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.01ЕФЧАЬсЯТШЯЮЊЁАЪЧЗёШЯПЩгыГЧЪаЕФгЕЖТЧщПігаЙиЁБ
D. ПЩвддкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.025ЕФЧАЬсЯТШЯЮЊЁАЪЧЗёШЯПЩгыГЧЪаЕФгЕЖТЧщПігаЙиЁБ
 ЯАЬтОЋбЁЯЕСаД№АИ
ЯАЬтОЋбЁЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌРтГЄЮЊ1ЃЈЕЅЮЛЃК![]() ЃЉЕФе§ЗНЬхФОПщОЙ§ЪЪЕБЧаИюЃЌЕУЕНМИКЮЬх
ЃЉЕФе§ЗНЬхФОПщОЙ§ЪЪЕБЧаИюЃЌЕУЕНМИКЮЬх![]() ЃЌвбжЊМИКЮЬх
ЃЌвбжЊМИКЮЬх![]() гЩСНИіЕзУцЯрЭЌЕФе§ЫФРтзЖзщГЩЃЌЕзУц
гЩСНИіЕзУцЯрЭЌЕФе§ЫФРтзЖзщГЩЃЌЕзУц![]() ЦНаагке§ЗНЬхЕФЯТЕзУцЃЌЧвИїЖЅЕуОљдке§ЗНЬхЕФУцЩЯЃЌдђМИКЮЬх
ЦНаагке§ЗНЬхЕФЯТЕзУцЃЌЧвИїЖЅЕуОљдке§ЗНЬхЕФУцЩЯЃЌдђМИКЮЬх![]() ЬхЛ§ЕФШЁжЕЗЖЮЇЪЧ________ЃЈЕЅЮЛЃК
ЬхЛ§ЕФШЁжЕЗЖЮЇЪЧ________ЃЈЕЅЮЛЃК![]() ЃЉЃЎ
ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
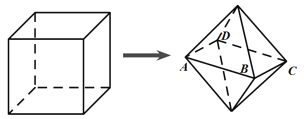
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
дкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌжБЯп
ЮЊВЮЪ§ЃЉЃЌжБЯп![]() гыЧњЯп
гыЧњЯп![]() ЃК
ЃК![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕу.
СНЕу.
ЃЈЂёЃЉЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈЂђЃЉдквд![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂЕФМЋзјБъЯЕжаЃЌЩшЕу
жсЕФе§АыжсЮЊМЋжсНЈСЂЕФМЋзјБъЯЕжаЃЌЩшЕу![]() ЕФМЋзјБъЮЊ
ЕФМЋзјБъЮЊ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕНЯпЖЮ
ЕНЯпЖЮ![]() жаЕу
жаЕу![]() ЕФОрРы.
ЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВЕФжааФдкзјБъдЕу![]() ЃЌНЙЕудк
ЃЌНЙЕудк![]() жсЩЯЃЌЖЬжсГЄЮЊ
жсЩЯЃЌЖЬжсГЄЮЊ![]() ЃЌЧвСНИіНЙЕуКЭЖЬжсЕФСНИіЖЫЕуЧЁЮЊвЛИіе§ЗНаЮЕФЖЅЕуЃЎ
ЃЌЧвСНИіНЙЕуКЭЖЬжсЕФСНИіЖЫЕуЧЁЮЊвЛИіе§ЗНаЮЕФЖЅЕуЃЎ
ЃЈ1ЃЉЧѓЭждВЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшЙ§гвНЙЕу![]() гы
гы![]() жсВЛДЙжБЕФжБЯпгыЭждВНЛгк
жсВЛДЙжБЕФжБЯпгыЭждВНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЎдкЯпЖЮ
СНЕуЃЎдкЯпЖЮ![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУвд
ЃЌЪЙЕУвд![]() ЁЂ
ЁЂ![]() ЮЊСкБпЕФЦНааЫФБпаЮЪЧСтаЮЃПШєДцдкЃЌЧѓГі
ЮЊСкБпЕФЦНааЫФБпаЮЪЧСтаЮЃПШєДцдкЃЌЧѓГі![]() ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌ
ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌ
ЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩшЕу![]() дкЭждВЩЯдЫЖЏЃЌ
дкЭждВЩЯдЫЖЏЃЌ![]() ЃЌЧвЕу
ЃЌЧвЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЕШгк
ЕФОрРыЕШгк![]() ЃЌЪдЧѓЖЏЕу
ЃЌЪдЧѓЖЏЕу![]() ЕФЙь
ЕФЙь
МЃЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкxOyЦНУцЩЯЃЌНЋЫЋЧњЯпЕФвЛжЇ![]()
![]() МАЦфНЅНќЯп
МАЦфНЅНќЯп![]() КЭжБЯп
КЭжБЯп![]() ЁЂ
ЁЂ![]() ЮЇГЩЕФЗтБеЭМаЮМЧЮЊDЃЌШчЭМжавѕгАВПЗжЃЌМЧDШЦyжса§зЊвЛжмЫљЕУЕФМИКЮЬхЮЊ
ЮЇГЩЕФЗтБеЭМаЮМЧЮЊDЃЌШчЭМжавѕгАВПЗжЃЌМЧDШЦyжса§зЊвЛжмЫљЕУЕФМИКЮЬхЮЊ![]() ЃЌЙ§
ЃЌЙ§![]()
![]() зї
зї![]() ЕФЫЎЦННиУцЃЌМЦЫуНиУцУцЛ§ЃЌРћгУзцдРэЕУГі
ЕФЫЎЦННиУцЃЌМЦЫуНиУцУцЛ§ЃЌРћгУзцдРэЕУГі![]() ЬхЛ§ЮЊ________
ЬхЛ§ЮЊ________

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћжБЯпy=kx+1гыдВx2+y2+kx+myЉ4=0НЛгкMЁЂNСНЕуЃЌЧвMЁЂNЙигкжБЯпx+y=0ЖдГЦЃЌдђВЛЕШЪНзщЃК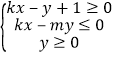 БэЪОЕФЦНУцЧјгђЕФУцЛ§ЪЧЃЈЁЁЃЉ
БэЪОЕФЦНУцЧјгђЕФУцЛ§ЪЧЃЈЁЁЃЉ
A.![]()
B.![]()
C.1
D.2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЖдгкКЏЪ§fЃЈxЃЉЖЈвхгђФкШЮвтЕФСНИіздБфСПЕФжЕx1 ЃЌ x2 ЃЌ ЕБx1ЃМx2ЪБЃЌЖМгаfЃЈx1ЃЉЁмfЃЈx2ЃЉЃЌЧвДцдкСНИіВЛЯрЕШЕФздБфСПжЕy1 ЃЌ y2 ЃЌ ЪЙЕУfЃЈy1ЃЉ=fЃЈy2ЃЉЃЌОЭГЦfЃЈxЃЉЮЊЖЈвхгђЩЯЕФВЛбЯИёЕФдіКЏЪ§ЃЎ
дђ Ђй ЃЌ Ђк
ЃЌ Ђк ЃЌ
ЃЌ
Ђл ЃЌ Ђм
ЃЌ Ђм![]() ЃЌ
ЃЌ
ЫФИіКЏЪ§жаЮЊВЛбЯИёдіКЏЪ§ЕФЪЧ ЃЌШєвбжЊКЏЪ§gЃЈxЃЉЕФЖЈвхгђЁЂжЕгђЗжБ№ЮЊAЁЂBЃЌA={1ЃЌ2ЃЌ3}ЃЌBAЃЌЧвgЃЈxЃЉЮЊЖЈвхгђAЩЯЕФВЛбЯИёЕФдіКЏЪ§ЃЌФЧУДетбљЕФgЃЈxЃЉга ИіЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЖўДЮКЏЪ§fЃЈxЃЉ=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгыжБЯпy=xЮоНЛЕуЃЌЯжгаЯТСаНсТлЃК
ЂйШєa=1ЃЌb=2ЃЌдђcЃО![]()
ЂкШєa+b+c=0ЃЌдђВЛЕШЪНfЃЈxЃЉЃОxЖдвЛЧаЪЕЪ§xЖМГЩСЂ
ЂлКЏЪ§gЃЈxЃЉ=ax2Љbx+cЕФЭМЯѓгыжБЯпy=ЉxвВвЛЖЈУЛгаНЛЕу
ЂмШєaЃО0ЃЌдђВЛЕШЪНf[fЃЈxЃЉ]ЃОxЖдвЛЧаЪЕЪ§xЖМГЩСЂ
ЂнЗНГЬf[fЃЈxЃЉ]=xвЛЖЈУЛгаЪЕЪ§Иљ
Цфжае§ШЗЕФНсТлЪЧ ЃЈаДГіЫљгае§ШЗНсТлЕФБрКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЧвЧњЯп
ЃЌЧвЧњЯп![]() дкЕу
дкЕу![]() ДІЕФЧаЯпЗНГЬЮЊ
ДІЕФЧаЯпЗНГЬЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§![]() ЕФжЕМАКЏЪ§
ЕФжЕМАКЏЪ§![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ2ЃЉжЄУїЃКЖдШЮвтЕФ![]() .
.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com