练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设＝(1，)，＝(0，1)，O为坐标原点，动点P(x，y)满足0≤·≤1，0≤·≤1，则z＝y－x的最大值是

    [　　]

    A．

    B．1

    C．－1

    D．－2

    答案：A
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知向量a＝(1,2)，b＝(0,1)，设u＝a＋kb，v＝2a－b，若u∥v，则实数k的值为________．

    查看答案和解析>>

    科目：高中数学 来源：2015届广东省高一暑假作业（六）必修4数学试卷（解析版） 题型：选择题

    已知||＝1，||＝，·＝0，点C在∠AOB内，且∠AOC＝30°.设＝m＋n (m、n∈R)，则等于(    )

    A．               B．3                C．             D．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年山西省高三2月月考文科数学试卷 题型：解答题

    （12分）设向量＝(1，cos2θ)，＝(2，1)，＝(4sinθ，1)，＝(sinθ，1)，其中θ∈(0，)．

    (1)求·－·的取值范围；

    (2)若函数f(x)＝|x－1|，比较f(·)与f(·)的大小．

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年江西省南昌市高三第一次月考理科数学卷 题型：选择题

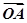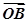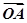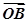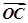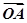    已知| |＝1，||＝，·＝0，点C在∠AOB内，且∠AOC＝30°，设＝m＋n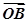(m，n∈R)，则等于  (　　)                                                       

    A.　　　　    　　B．3               C.                   D.

     

    查看答案和解析>>

    科目：高中数学 来源：2013届黑龙江虎林高中高二下学期期中理科数学试卷（解析版） 题型：解答题

    已知函数f(x)＝alnx－x2＋1.

    (1)若曲线y＝f(x)在x＝1处的切线方程为4x－y＋b＝0，求实数a和b的值；

    (2)若a<0，且对任意x1、x2∈(0，＋∞)，都|f(x1)－f(x2)|≥|x1－x2|，求a的取值范围．

    【解析】第一问中利用f′(x)＝－2x(x>0)，f′(1)＝a－2，又f(1)＝0，所以曲线y＝f(x)在x＝1处的切线方程为y＝(a－2)(x－1)，即(a－2)x－y＋2－a＝0，

    由已知得a－2＝4,2－a＝b，所以a＝6，b＝－4.

    第二问中，利用当a<0时，f′(x)<0，∴f(x)在(0，＋∞)上是减函数，

    不妨设0<x1≤x2，则|f(x1)－f(x2)|＝f(x1)－f(x2)，|x1－x2|＝x2－x1，

    ∴|f(x1)－f(x2)|≥|x1－x2|等价于f(x1)－f(x2)≥x2－x1，

    即f(x1)＋x1≥f(x2)＋x2，结合构造函数和导数的知识来解得。

    (1)f′(x)＝－2x(x>0)，f′(1)＝a－2，又f(1)＝0，所以曲线y＝f(x)在x＝1处的切线方程为y＝(a－2)(x－1)，即(a－2)x－y＋2－a＝0，

    由已知得a－2＝4,2－a＝b，所以a＝6，b＝－4.

    (2)当a<0时，f′(x)<0，∴f(x)在(0，＋∞)上是减函数，

    不妨设0<x1≤x2，则|f(x1)－f(x2)|＝f(x1)－f(x2)，|x1－x2|＝x2－x1，

    ∴|f(x1)－f(x2)|≥|x1－x2|等价于f(x1)－f(x2)≥x2－x1，即f(x1)＋x1≥f(x2)＋x2，

    令g(x)＝f(x)＋x＝alnx－x2＋x＋1，g(x)在(0，＋∞)上是减函数，

    ∵g′(x)＝－2x＋1＝(x>0)，

    ∴－2x2＋x＋a≤0在x>0时恒成立，

    ∴1＋8a≤0，a≤－，又a<0，

    ∴a的取值范围是

     

    查看答案和解析>>

    同步练习册答案