
【题目】在平面直角坐标系xOy中,已知直线![]() 与圆O:
与圆O:![]() 相切.
相切.
(1)直线l过点(2,1)且截圆O所得的弦长为![]() ,求直线l的方程;
,求直线l的方程;
(2)已知直线y=3与圆O交于A,B两点,P是圆上异于A,B的任意一点,且直线AP,BP与y轴相交于M,N点.判断点M、N的纵坐标之积是否为定值?若是,求出该定值;若不是,说明理由.
【答案】(1)![]() 或
或![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)记圆心到直线l的距离为d,利用垂径定理求得d.当直线l与x轴垂直时,直线l的方程为x=2,满足题意;当直线l与x轴不垂直时,设直线l的方程为y﹣1=k(x﹣2),利用圆心到直线的距离列式求得k,则直线方程可求;
(2)设P(x1,y1),由直线y=3与圆O交于A、B两点,不妨取A(1,3),B(﹣1,3),分别求出直线PA、PB的方程,进一步得到M,N的坐标,由P在圆上,整体运算可得![]() 为定值.
为定值.
∵直线x﹣3y﹣10=0与圆O:x2+y2=r2(r>0)相切,
∴圆心O到直线x﹣3y﹣10=0的距离为r=![]() .
.
(1)记圆心到直线l的距离为d,∴d=![]() .
.
当直线l与x轴垂直时,直线l的方程为x=2,满足题意;
当直线l与x轴不垂直时,设直线l的方程为y﹣1=k(x﹣2),即kx﹣y+(1﹣2k)=0.
∴![]() ,解得k=﹣
,解得k=﹣![]() ,此时直线l的方程为3x+4y﹣10=0.
,此时直线l的方程为3x+4y﹣10=0.
综上,直线l的方程为x=2或3x+4y﹣10=0;
(2)点M、N的纵坐标之积为定值10.
设P(x1,y1),
∵直线y=3与圆O交于A、B两点,不妨取A(1,3),B(﹣1,3),
∴直线PA、PB的方程分别为y﹣3=![]() ,y﹣3=
,y﹣3=![]() .
.
令x=0,得M(0,![]() ),N(0,
),N(0,![]() ),
),
则![]() (*).
(*).
∵点P(x1,y1)在圆C上,∴![]() ,即
,即![]() ,
,
代入(*)式,得![]() 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】在平面角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度得到曲线
个单位长度得到曲线![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)已知![]() 为曲线
为曲线![]() 上的动点,
上的动点, ![]() 两点的极坐标分别为
两点的极坐标分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队进行一场排球比赛,根据以往经验,单局比赛甲队胜乙队的概率为![]() .本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响且无平局.求:
.本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响且无平局.求:
(1)前三局比赛甲队领先的概率;
(2)设本场比赛的局数为![]() ,求
,求![]() 的概率分布和数学期望. (用分数表示)
的概率分布和数学期望. (用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬中华民族优秀传统文化,树立正确的价值导向,落实立德树人根本任务,某市组织30000名高中学生进行古典诗词知识测试,根据男女学生人数比例,使用分层抽样的方法从中随机抽取100名学生,记录他们的分数,整理所得频率分布直方图如图:

(Ⅰ)规定成绩不低于60分为及格,不低于85分为优秀,试估计此次测试的及格率及优秀率;
(Ⅱ)试估计此次测试学生成绩的中位数;
(Ⅲ)已知样本中有![]() 的男生分数不低于80分,且样本中分数不低于80分的男女生人数相等,试估计参加本次测试30000名高中生中男生和女生的人数.
的男生分数不低于80分,且样本中分数不低于80分的男女生人数相等,试估计参加本次测试30000名高中生中男生和女生的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个半圆中有两个互切的内切半圆,由三个半圆弧围成曲边三角形,作两个内切半圆的公切线把曲边三角形分隔成两块,阿基米德发现被分隔的这两块的内切圆是同样大小的,由于其形状很像皮匠用来切割皮料的刀子,他称此为“皮匠刀定理”,如图,若![]() ,则阴影部分与最大半圆的面积比为( )
,则阴影部分与最大半圆的面积比为( )
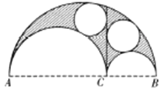
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,下述四个结论:
,下述四个结论:
①![]() 是偶函数;
是偶函数;
②![]() 的最小正周期为
的最小正周期为![]() ;
;
③![]() 的最小值为0;
的最小值为0;
④![]() 在
在![]() 上有3个零点
上有3个零点
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个半圆中有两个互切的内切半圆,由三个半圆弧围成曲边三角形,作两个内切半圆的公切线把曲边三角形分隔成两块,阿基米德发现被分隔的这两块的内切圆是同样大小的,由于其形状很像皮匠用来切割皮料的刀子,他称此为“皮匠刀定理”,如图,若![]() ,则阴影部分与最大半圆的面积比为( )
,则阴影部分与最大半圆的面积比为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com