【题目】某超市在2017年五一正式开业，开业期间举行开业大酬宾活动，规定：一次购买总额在区间
内者可以参与一次抽奖，根据统计发现参与一次抽奖的顾客每次购买金额分布情况如下：
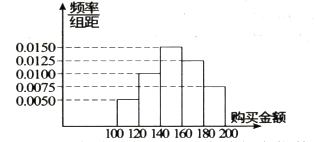
（1）求参与一次抽奖的顾客购买金额的平均数与中位数（同一组中的数据用该组区间的中点值作代表，结果保留到整数）；
（2）若根据超市的经营规律，购买金额
与平均利润
有以下四组数据：
试根据所给数据，建立
关于
的线性回归方程
，并根据（1）中计算的结果估计超市对每位顾客所得的利润.
参考公式：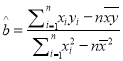 
， 
.
【答案】（1）见解析.（2）
.20.45（元）.
【解析】【试题分析】（1）计算出每组的频率，用每组中点值乘以频率然后相加可得到平均数的估计值.中位数是使得左右两边频率为
的位置，先确定
在第三组，然后利用小长方形的面积计算出中位数的位置.（2）利用回归直线方程公式，代入数据计算出回归直线方程.
【试题解析】
（1）由所给频率分布直方图可知，这5组数据的频率分别为：0.1,0.2,0.3,0.25,0.15，故这组数据的平均数为：
；
∵
， 
.
∴这组数据的中位数为： 
.
（2）由所给数据可得： 
， 
，
， 
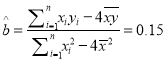，∴回归直线方程为： 
.
由此可以估计，把
代入可得每位顾客贡献给超市的平均利润为：
（元）.
黄冈创优卷系列答案科目：高中数学 来源： 题型：
【题目】已知中心在原点O，左焦点为F1(－1,0)的椭圆C的左顶点为A，上顶点为B，F1到直线AB的距离为
|OB|.
(1)求椭圆C的方程；
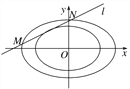
(2)如图，若椭圆
，椭圆
，则称椭圆C2是椭圆C1的λ倍相似椭圆．已知C2是椭圆C的3倍相似椭圆，若椭圆C的任意一条切线l交椭圆C2于两点M、N，试求弦长|MN|的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的图象与
轴正半轴交点的横坐标依次构成一个公差为
的等差数列，把函数
的图象沿
轴向右平移
个单位，得到函数
的图象，则下列叙述不正确的是（ ）
A. 
的图象关于点
对称 B. 
的图象关于直线
对称
C. 
在
上是增函数 D. 
是奇函数
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
的左、右焦点分别为
和
，离心率是
，直线
过点
交椭圆于
， 
两点，当直线
过点
时， 
的周长为
.
（Ⅰ）求椭圆
的标准方程；
（Ⅱ）当直线
绕点
运动时，试求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知直角坐标系中动点
，参数
，在以原点为极点、
轴正半轴为极轴所建立的极坐标系中，动点
在曲线
： 
上.
（1）求点
的轨迹
的普通方程和曲线
的直角坐标方程；
（2）若动点
的轨迹
和曲线
有两个公共点，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形的面积可无限接近圆的面积，并创立了“割圆术”，利用“割圆术”，刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”，利用刘徽的“割圆术”思想设计的一个程序框图，则输出的值为（ ）
（参考数据： 
）
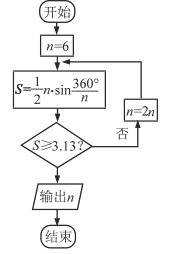
A. 12 B. 24 C. 48 D. 96
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
