
【题目】己知![]() ,点
,点![]() 是直线
是直线![]() 与圆
与圆![]() 的公共点,则
的公共点,则![]() 的最大值为( ).
的最大值为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增.函数
单调递增.函数 .
.
(1)请写出函数![]() 与函数
与函数![]() 在
在![]() 的单调区间;(只写结论,不需证明)
的单调区间;(只写结论,不需证明)
(2)求函数![]() 的最大值和最小值;
的最大值和最小值;
(3)讨论方程![]() 实根的个数.
实根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为提高员工的综合素质,聘请专业机构对员工进行专业技术培训,其中培训机构费用成本为12000元.公司每位员工的培训费用按以下方式与该机构结算:若公司参加培训的员工人数不超过30人时,每人的培训费用为850元;若公司参加培训的员工人数多于30人,则给予优惠:每多一人,培训费减少10元.已知该公司最多有60位员工可参加培训,设参加培训的员工人数为![]() 人,每位员工的培训费为
人,每位员工的培训费为![]() 元,培训机构的利润为
元,培训机构的利润为![]() 元.
元.
(1)写出![]() 与
与![]()
![]() 之间的函数关系式;
之间的函数关系式;
(2)当公司参加培训的员工为多少人时,培训机构可获得最大利润?并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的短轴长为2,过上顶点E和右焦点F的直线与圆M:x2+y2﹣4x﹣2y+4=0相切.
(a>b>0)的短轴长为2,过上顶点E和右焦点F的直线与圆M:x2+y2﹣4x﹣2y+4=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l过点(1,0),且与椭圆C交于点A,B,则在x轴上是否存在一点T(t,0)(t≠0),使得不论直线l的斜率如何变化,总有∠OTA=∠OTB (其中O为坐标原点),若存在,求出 t的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设![]() 米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
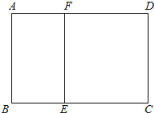
(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1= ![]() (n∈N*).
(n∈N*).
(1)求证:{ ![]() +
+ ![]() }为等比数列,并求{an}的通项公式an;
}为等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) ![]() an , 求数列{bn}的前n项和Tn .
an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数h(x)=lnx+ ![]() .
.
(1)函数g(x)=h(2x+m),若x=1是g(x)的极值点,求m的值并讨论g(x)的单调性;
(2)函数φ(x)=h(x)﹣ ![]() +ax2﹣2x有两个不同的极值点,其极小值为M,试比较2M与﹣3的大小关系,并说明理由.
+ax2﹣2x有两个不同的极值点,其极小值为M,试比较2M与﹣3的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com