练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列命题:

    ①在一个列联表中,由计算得,则有的把握确认这两类指标间有关联

    ②若二项式的展开式中所有项的系数之和为，则展开式中的系数是

    ③随机变量服从正态分布,则

    ④若正数满足，则的最小值为

    其中正确命题的序号为( )

    A. ①②③B. ①③④C. ②④D. ③④

    【答案】B

    【解析】

    根据可知①正确；代入可求得，利用展开式通项，可知时，为含的项，代入可求得系数为，②错误；根据正态分布曲线的对称性可知③正确；由，利用基本不等式求得最小值，可知④正确.

    ①，则有的把握确认这两类指标间有关联，①正确；

    ②令，则所有项的系数和为：，解得：

    则其展开式通项为：

    当，即时，可得系数为：，②错误；

    ③由正态分布可知其正态分布曲线对称轴为 ，③正确；

    ④

    ， ，

    （当且仅当，即时取等号）

    ，④正确.

    本题正确选项：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程，下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是（ ）

    A. 消耗1升汽油，乙车最多可行驶5千米

    B. 以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多

    C. 甲车以80千米/小时的速度行驶1小时，消耗10升汽油

    D. 某城市机动车最高限速80千米/小时. 相同条件下，在该市用丙车比用乙车更省油

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元。

    （1）分别写出两类产品的收益与投资额的函数关系式；

    （2）该家庭现有20万元资金，全部用于理财投资，怎样分配资金才能获得最大收益？其最大收益为多少万元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱台中， 侧面与侧面是全等的梯形，若,且.

    （Ⅰ）若， ，证明： ∥平面；

    （Ⅱ）若二面角为，求平面与平面所成的锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《九章算术》里有一段叙述：今有良马与驽马发长安至齐，齐去长安一千一百二十五里，良马初日行一百零三里，日增十三里；驽马初日行九十七里，日减半里；良马先至齐，复还迎驽马，二马相逢.根据该问题设计程序框图如下，若输入，则输出的值是（ ）

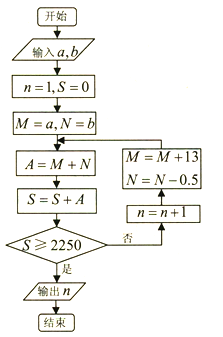
    A. 8 B. 9 C. 12 D. 16

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，ABCD－A1B1C1D1是长方体，O是B1D1的中点，直线A1C交平面AB1D1于点M，则下列结论正确是( )

    A.A，M，O三点共线B.A，M，O，A1不共面

    C.A，M，C，O不共面D.B，B1，O，M共面

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4－5：不等式选讲

    设函数．

    （Ⅰ）解不等式；

    （Ⅱ）若对一切实数均成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】时下，租车自驾游已经比较流行了．某租车点的收费标准为：不超过天收费元，超过天的部分每天收费元（不足天按天计算）．甲、乙两人要到该租车点租车自驾到某景区游览，他们不超过天还车的概率分别为和，天以上且不超过天还车的概率分别为和，两人租车都不会超过天．

    （1）求甲所付租车费比乙多的概率；

    （2）设甲、乙两人所付的租车费之和为随机变量,求的分布列和数学期望.

    查看答案和解析>>

    同步练习册答案