Question

【题目】如图，在四棱台ABCD﹣A1B1C1D1中，平面BCC1B1⊥平面ABCD，四边形ABCD为平行四边形，四边形BCC1B1为等腰梯形，BC=4，B1C1=C1C=2，AB=5，AC⊥BC．

（1）求证：BC1⊥平面ACC1；
（2）求直线BC1与平面ADD1A1所成的角的正弦值．

Answer 1

【答案】
（1）证明：如图，在BCC1B1内过点C1作C1M⊥BC于点M，

因为四边形CC1B1为等腰梯形，BC=4，B1C1=C1C=2，所以MC=1，MB=3，

在Rt△C1MC中，知MC1= ，所以BC1=2 ，

可得BC1⊥CC1，

又因AC⊥BC，平面BCC1B1⊥平面ABCD，

平面BCC1B1∩平面ABCD=BC，所以AC⊥平面BCC1B1，

因为BC1平面BCC1B1，所以AC⊥BC1，

又因AC∩CC1=C，

所以BC1⊥平面ACC1

（2）解：延长BB1，CC1，AA1，DD1知相交于一点，记该点为P，取BC中点O，

在四棱台中，PO⊥BC，

又因平面BCC1B1⊥平面ABCD，所以PO⊥平面ABCD，

取AB中点N，知ON∥AC，且ON⊥BC，所以以O为坐标原点，建立空间直角坐标系，则A（3，﹣2，0），B（0，2，0），C（0，﹣2，0），P（0，0，2 ）， ，

所以 =（0，﹣3， ） =（3，﹣2，﹣2 ）， = =（0，﹣4，0）．

设平面ADD1A1的法向量为 =（x，y，z），则 ，可取 =（2，0， ）

所以cos＜ ， ＞= ，故直线BC1与平面ADD1A1所成的角的正弦值为 ．

【解析】（1）在BCC1B1内过点C1作C1M⊥BC于点M，证明BC1⊥CC1 ， AC⊥BC1 ， 即可证明BC1⊥平面ACC1；（2）求出平面ADD1A1的法向量，即可求直线BC1与平面ADD1A1所成的角的正弦值．
【考点精析】关于本题考查的直线与平面垂直的判定和空间角的异面直线所成的角，需要了解一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则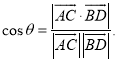才能得出正确答案．