练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在研究色盲与性别的关系调查中，调查了男性480人，其中有38人患色盲，调查的520个女性中6人患色盲．　

    （Ⅰ）根据题中数据建立一个的列联表；

    （Ⅱ）在犯错误的概率不超过0.001的前提下，能否认为“性别与患色盲有关系”？

    附：参考公式，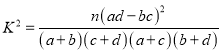

    【答案】（1）见解析（2）可以认为

    【解析】试题分析：（1）根据题意计算不患色盲的男人数及女人数，列出的列联表；（2）代入参考公式，计算，对照参考数据判断是否相关.

    试题解析：（Ⅰ）

    患色盲

    不患色盲

    总计

    男

    38

    442

    480

    女

    6

    514

    520

    总计

    44

    956

    1000

    （Ⅱ）假设：“性别与患色盲没有关系”．

    先算出的观测值：

    ，

    则有，即成立的概率不超过0.001，

    故在犯错的概率不超过0.001的前提下，可以认为“性别与患色盲有关系”．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，为的重心，.

    （1）求证：平面；

    （2）若侧面底面，，，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图, 在△中, 点在边上, .

    （Ⅰ）求；

    （Ⅱ）若△的面积是, 求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

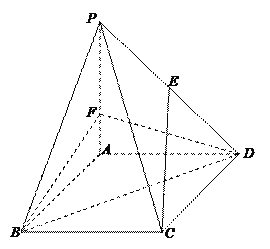
    【题目】如图，在边长为3的菱形ABCD中，∠ABC=60°，平面ABCD，且，E为PD中点，F在棱PA上，且.

    （1）求证：CE∥平面BDF；

    （2）求点P到平面BDF的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是公差为的等差数列，是公比为的等比数列. 记.

    （1）求证: 数列为等比数列；

    （2）已知数列的前项分别为.

    ①求数列和的通项公式；

    ②是否存在元素均为正整数的集合，使得数列等差数列？证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体中，为棱的中点.

    求证：（1）平面；

    （2）平面平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数.

    （1）求证：曲线在点处的切线过定点；

    （2）若是在区间上的极大值，但不是最大值，求实数的取值范围；

    （3）求证：对任意给定的正数，总存在，使得在上为单调函数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数，若在定义域内存在实数，满足，则称为“局部奇函数”．

    为定义在上的“局部奇函数”；

    曲线与轴交于不同的两点；

    若为假命题， 为真命题，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量，函数，若函数的图象与轴的两个相邻交点的距离为.

    （1）求函数的单调区间；

    （2）若时， ，求的值.

    （3）若，且有且仅有一个实根，求实数的值.

    查看答案和解析>>

    同步练习册答案