
【题目】如果对于函数f(x)定义域内任意的两个自变量的值x1 , x2 , 当x1<x2时,都有f(x1)≤f(x2),且存在两个不相等的自变量值y1 , y2 , 使得f(y1)=f(y2),就称f(x)为定义域上的不严格的增函数.
则 ① , ②
, ② ,
,
③ , ④
, ④![]() ,
,
四个函数中为不严格增函数的是 ,若已知函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,那么这样的g(x)有 个.
【答案】①③;9
【解析】解:由已知中:函数f(x)定义域内任意的两个自变量的值x1 , x2 ,
当x1<x2时,都有f(x1)≤f(x2),
且存在两个不相等的自变量值y1 , y2 , 使得f(y1)=f(y2),
就称f(x)为定义域上的不严格的增函数.
① , 满足条件,为定义在R上的不严格的增函数;
, 满足条件,为定义在R上的不严格的增函数;
② , 当x1=﹣
, 当x1=﹣![]() , x2∈(﹣
, x2∈(﹣![]() ,
, ![]() ),f(x1)>f(x2),故不是不严格的增函数;
),f(x1)>f(x2),故不是不严格的增函数;
③ , 满足条件,为定义在R上的不严格的增函数;
, 满足条件,为定义在R上的不严格的增函数;
④![]() , 当x1=
, 当x1=![]() , x2∈(1,
, x2∈(1,![]() ),f(x1)>f(x2),故不是不严格的增函数;
),f(x1)>f(x2),故不是不严格的增函数;
故已知的四个函数中为不严格增函数的是①③;
∵函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,
则满足条件的函数g(x)有:
g(1)=g(2)=g(3)=1,
g(1)=g(2)=g(3)=2,
g(1)=g(2)=g(3)=3,
g(1)=g(2)=1,g(3)=2,
g(1)=g(2)=1,g(3)=3,
g(1)=g(2)=2,g(3)=3,
g(1)=1,g(2)=g(3)=2,
g(1)=1,g(2)=g(3)=3,
g(1)=2,g(2)=g(3)=3,
故这样的函数共有9个,
所以答案是:①③;9.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的短轴一个端点到右焦点F的距离为2,且过点
=1(a>b>0)的短轴一个端点到右焦点F的距离为2,且过点 ![]() .
.
(1)求椭圆C的方程;
(2)设M,N为椭圆C上不同的两点,A,B分别为椭圆C上的左右顶点,直线MN既不平行与坐标轴,也不过椭圆C的右焦点F,若∠AFM=∠BFN,求证:直线MN过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在,很多人都喜欢骑“共享单车”,但也有很多市民并不认可.为了调查人们对这种交通方式的认可度,某同学从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20名市民,得到了一个市民是否认可的样本,具体数据如下![]() 列联表:
列联表:
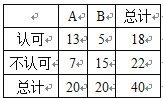
附:![]() ,
,![]() .
.

根据表中的数据,下列说法中,正确的是( )
A. 没有95% 以上的把握认为“是否认可与城市的拥堵情况有关”
B. 有99% 以上的把握认为“是否认可与城市的拥堵情况有关”
C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”
D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以坐标原点
为极点,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线
轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若曲线![]() 上的点到直线
上的点到直线![]() 的最大距离为6,求实数
的最大距离为6,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了调研当代中国高中生的平均年龄,从各地多所高中随机抽取了40名学生进行年龄统计,得到结果如下表所示:
年龄(岁) |
|
|
|
|
|
数量 | 6 | 10 | 12 | 8 | 4 |
(Ⅰ)若同一组数据用该组区间的中点值代表,试估计这批学生的平均年龄;
(Ⅱ)若在本次抽出的学生中随机挑选2人,记年龄在![]() 间的学生人数为
间的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,对角线
是菱形,对角线![]() ,
,![]() 交于点
交于点![]() .
.

(Ⅰ)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,求证:
,求证:![]() ;
;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() (异于点
(异于点![]() ),使得
),使得![]() 平面
平面![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹马进行一场比赛,齐王获胜的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取![]() 件,测量这些产品的一项质量指标值,由测量结果得如频率分布直方图:
件,测量这些产品的一项质量指标值,由测量结果得如频率分布直方图:
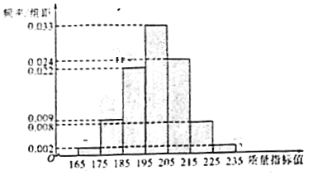
(1)求这![]() 件产品质量指标值的样本平均数
件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)由直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
①利用该正态分布,求![]() ;
;
②某用户从该企业购买了![]() 件这种产品,记
件这种产品,记![]() 表示这
表示这![]() 件产品中质量指标值位于区间
件产品中质量指标值位于区间![]() 的产品件数.利用①的结果,求
的产品件数.利用①的结果,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com