
【题目】给定![]() ,
,![]() ,
,![]() ,
,![]() 所对的边分别是
所对的边分别是![]() ,
,![]() ,
,![]() ,在
,在![]() 所在平面作直线
所在平面作直线![]() 与
与![]() 的某两边相交,沿
的某两边相交,沿![]() 将
将![]() 折成一个空间图形,将由
折成一个空间图形,将由![]() 分成的小三角形的不在
分成的小三角形的不在![]() 上的顶点与另一部分的顶点连接,形成一个三棱锥或四棱锥。问:
上的顶点与另一部分的顶点连接,形成一个三棱锥或四棱锥。问:
(1)当![]() 时,
时,![]() 如何作,并折成何种锥体,才能使所得锥体体积最大?(需详证)
如何作,并折成何种锥体,才能使所得锥体体积最大?(需详证)
(2)当![]() 时,
时,![]() 如何作,并折成何种锥体,才能使所得锥体体积最大?(叙述结果,不要证明)
如何作,并折成何种锥体,才能使所得锥体体积最大?(叙述结果,不要证明)
【答案】(1)见解析;(2)见解析
【解析】
(1)由棱锥的体积![]() 高
高![]() 底面积,易知要使锥体体积最大,则折线的两部分所在平面互相垂直。
底面积,易知要使锥体体积最大,则折线的两部分所在平面互相垂直。

如图所设,![]() ,
,
![]()
于是,当![]() 沿
沿![]() 折起,并与
折起,并与![]() 成直二面角时,所形成的锥体体积为
成直二面角时,所形成的锥体体积为
![]()
![]()
![]()
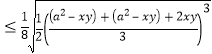
![]()
![]() 当且仅当
当且仅当![]() 且
且![]() ,即
,即![]() 时成立。
时成立。
所以,当![]() 与
与![]() ,
,![]() 边交于
边交于![]() ,
,![]() ,
,![]() ,并且
,并且![]() 所在平面和四边形
所在平面和四边形![]() 所在平面垂直时,棱锥体积最大。
所在平面垂直时,棱锥体积最大。
(2)当![]() 和
和![]() ,
,![]() 边交于
边交于![]() ,
,![]() ,
,![]() ,并且
,并且![]() 所在平面和四边形
所在平面和四边形![]() 所在平面垂直时,锥体体积最大。
所在平面垂直时,锥体体积最大。
(2)的证明提示:
分三步讨论。
第一步:证明满足条件的![]() 必定截
必定截![]() 成一个以
成一个以![]() 为底的等腰三角形。
为底的等腰三角形。
1.如图,如果![]() ,要证明当
,要证明当![]() 时,
时,![]() 为最大。
为最大。

2.如果![]() (注意
(注意![]() ),则由所给条件
),则由所给条件![]() ,有
,有![]() 。因此,当
。因此,当![]() 个
个![]() 重合时,
重合时,![]() 最大。
最大。
3.如果从![]() 点或
点或![]() 点出发考虑,我们也可以得到类似结构。
点出发考虑,我们也可以得到类似结构。
第二步:证明![]() 为问题要求的位置时,
为问题要求的位置时,![]() 必与
必与![]() 的两邻边相交于
的两邻边相交于![]() ,
,![]() ,并且
,并且![]() 。
。
第三步:讨论![]() 的具体位置。
的具体位置。


科目:高中数学 来源: 题型:
【题目】设![]() 。
。![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中的数所成的数列,它包含
中的数所成的数列,它包含![]() 的不以1结尾的任何排列,即对于
的不以1结尾的任何排列,即对于![]() 的四个数的任意一个不以1结尾的排列
的四个数的任意一个不以1结尾的排列![]() ,
,![]() ,都有
,都有![]() ,
,![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,并且
,并且![]() ,求这种数列的项数
,求这种数列的项数![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知真命题:“函数![]() 的图象关于点
的图象关于点![]() 成中心对称图形”的等价条件为“函数
成中心对称图形”的等价条件为“函数![]() 是奇函数”.
是奇函数”.
(1)将函数![]() 的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数
的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数![]() 图象对称中心的坐标;
图象对称中心的坐标;
(2)已知命题:“函数![]() 的图象关于某直线成轴对称图象”的等价条件为“存在实数a和b,使得函数
的图象关于某直线成轴对称图象”的等价条件为“存在实数a和b,使得函数![]() 是偶函数”.断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
是偶函数”.断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军在网上经营了一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元/千克.为了增加销量,张军对以上四种干果进行促销,若一次性购买干果的总价达到150元,顾客就少付x(x∈Z)元,每笔订单顾客在网上支付成功后,张军会得到支付款的80%.
①当x=15时,顾客一次性购买松子和腰果各1千克,需要支付_________________元;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销的总价的70%,则x的最大值为___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+1,g(x)=4x+1,的定义域都是集合A,函数f(x)和g(x)的值域分别为S和T,
(1)若A=[1,2],求S∩T
(2)若A=[0,m]且S=T,求实数m的值
(3)若对于集合A的任意一个数x的值都有f(x)=g(x),求集合A.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com