
【题目】已知数列![]() 满足
满足![]()
(1)当![]() 时,写出
时,写出![]() 所有可能的值;
所有可能的值;
(2)当![]() 时,若
时,若![]() 且
且![]() 对任意
对任意![]() 恒成立,求数列
恒成立,求数列![]() 的通项公式;
的通项公式;
(3)记数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 分别构成等差数列,求
分别构成等差数列,求![]() .
.
科目:高中数学 来源: 题型:
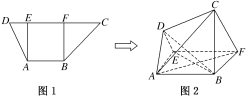
【题目】如图1,在高为2的梯形ABCD中,AB∥CD,AB=2,CD=5,过A,B分别作AE⊥CD,BF⊥CD,垂足分别为E,F.已知DE=1,将梯形ABCD沿AE,BF同侧折起,得空间几何体ADEBCF,如图2.若DE∥CF,CD=![]() ,在线段AB上是否存在点P,使得CP与平面ACD所成角的正弦值为
,在线段AB上是否存在点P,使得CP与平面ACD所成角的正弦值为![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】同学们有没有读过莎士比亚的名剧《威尼斯商人》?数学家斯摩林在剧中增加了一个情节:安东尼奥到鲍西娅家向她求婚,鲍西娅拿出一金、一银、一铝三个盒子,说:“每只盒子上写了一句话,但只有一句是真的.谁能猜中我的肖象在哪只盒子中,才能做我的丈夫”.如果你是聪明、政治的安东尼奥,请问肖象在哪个盒子内?(请从金盒、银盒、铝盒中选择一个填在横线上)________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长AB=3,侧棱AA1=2,E是棱CC1的中点,点F满足![]() =2
=2![]() .
.
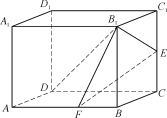
(1)求异面直线FE和DB1所成角的余弦值;
(2)记二面角E-B1F-A的大小为θ,求|cosθ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD所在平面垂直直角梯形ABPE所在的平面于直线AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.
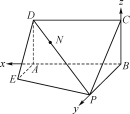
(1)求平面PCD与平面ABPE所成的二面角的余弦值;
(2)在线段PD上是否存在一点N,使得直线BN与平面PCD所成角的正弦值等于![]() ?若存在,试确定点N的位置;若不存在,请说明理由.
?若存在,试确定点N的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着![]() 网络的普及和智能手机的更新换代,各种方便的
网络的普及和智能手机的更新换代,各种方便的![]() 相继出世,其功能也是五花八门.某大学为了调查在校大学生使用
相继出世,其功能也是五花八门.某大学为了调查在校大学生使用![]() 的主要用途,随机抽取了
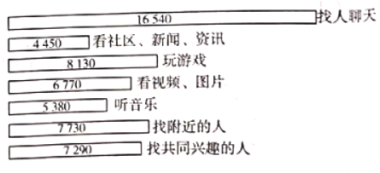
的主要用途,随机抽取了![]() 名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
①可以估计使用![]() 主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
②可以估计不足![]() 的大学生使用
的大学生使用![]() 主要玩游戏;
主要玩游戏;
③可以估计使用![]() 主要找人聊天的大学生超过总数的
主要找人聊天的大学生超过总数的![]() .
.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果一个数列从第2项起,每一项与它前一项的差都大于或等于2,则称这个数列为“D数列”.
(1)若首项为1的等差数列![]() 的每一项均为正整数,且数列
的每一项均为正整数,且数列![]() 为“D数列”,其前n项和
为“D数列”,其前n项和![]() 满足
满足![]() (
(![]() ),求数列
),求数列![]() 的通项公式;
的通项公式;
(2)已知等比数列![]() 的每一项均为正整数,且数列
的每一项均为正整数,且数列![]() 为“D数列”,
为“D数列”,![]() ,设
,设 (
(![]() ),试判断数列
),试判断数列![]() 是否为“D数列”,并说明理由.
是否为“D数列”,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com