
���� ��1���������ַ��̵Ļ�������������д��ֱ��l����ͨ���̺�����C��ֱ�����귽�̣�
��2������P��-1��0������ֱ��lƽ�е�ֱ��l1�ķ���Ϊx-y+1=0��������ľ࣬����ֱ�߷��̣����ɽ�����⣮
��� �⣺��1��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}x=2+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$��tΪ����������ȥ�������ɵ���ͨ����l��x-y-2=0��
����C�ļ����귽��Ϊ��=8cos�ȣ�����2=8��cos�ȣ���Ϊֱ�����귽��Ϊ x2+y2=8x��������x-4��2+y2=16
��2������P��-1��0������ֱ��lƽ�е�ֱ��l1�ķ���Ϊx-y+1=0��
��Բ�ĵ�ֱ�ߵľ���d=$\frac{5}{\sqrt{2}}$����|AB|=2$\sqrt{16-\frac{25}{2}}$=$\sqrt{14}$��
����AB���е�ΪQ����|PQ|=$\sqrt{25-\frac{25}{2}}$=$\frac{5}{2}\sqrt{2}$��
��|PA|+|PB|=2|PQ|=$5\sqrt{2}$��
���ɣ�2��֪$|PQ|=\frac{{5\sqrt{2}}}{2}$��ֱ��CQ�ķ���Ϊx+y-4=0����x-y+1=0�������ɵõ�Q������$Q��\frac{3}{2}��\frac{5}{2}��$��
���� ���⿼�����ַ��̵Ļ���������ֱ����Բ��λ�ù�ϵ������ѧ���ļ��������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x�����溯�� | B�� | f��x����ż���� | ||
| C�� | f��x���Ƿ����ż���� | D�� | f��x�������溯������ż���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+y=0 | B�� | x-y=0 | C�� | x-y+1=0 | D�� | x+y-1=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
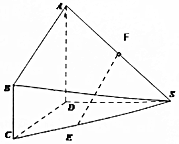 ��ͼ���ڼ�����SABCD�У�AD��ƽ��SCD��BC��AD��AD=DC=2��BC=1����SD=2����SDC=120�㣬F��SA���е㣬E��SC�ϣ�AE=$\sqrt{5}$��
��ͼ���ڼ�����SABCD�У�AD��ƽ��SCD��BC��AD��AD=DC=2��BC=1����SD=2����SDC=120�㣬F��SA���е㣬E��SC�ϣ�AE=$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��2 | B�� | m��1��m��2 | C�� | -1��m��2 | D�� | m��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | ${log_3}\frac{1}{2}$ | C�� | log32 | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com