

分析 根据cosC,cos∠DBC的值,便可求出cos$∠BDC=-\frac{1}{2}$,从而求出sin∠BDC的值,可设DC=x,BC=a,在△BDC中,由正弦定理即可得出a=$\sqrt{7}x$,而在△ABC中,根据余弦定理即可求出x=1,从而得出AD,CB的值,这样进行数量积的计算即可求出$\overrightarrow{AD}•\overrightarrow{CB}$的值.
解答 解:△BDC中,∵$cosC=\frac{2\sqrt{7}}{7}$,$cos∠DBC=\frac{5\sqrt{7}}{14}$;
∴$sinC=\frac{\sqrt{21}}{7},sin∠DBC=\frac{\sqrt{21}}{14}$;
∠BDC=π-(C+∠DBC);
∴cos∠BDC=-cos(C+∠DBC)
=sinCsin∠DBC-cosCcos∠DBC
=$\frac{\sqrt{21}}{7}×\frac{\sqrt{21}}{14}-\frac{2\sqrt{7}}{7}×\frac{5\sqrt{7}}{14}$
=$-\frac{1}{2}$;
∴$sin∠BDC=\frac{\sqrt{3}}{2}$;
设DC=x,BC=a;
在△BDC中,由正弦定理得:$\frac{x}{\frac{\sqrt{21}}{14}}=\frac{a}{\frac{\sqrt{3}}{2}}$;
∴$a=\sqrt{7}x$;
在△ABC中,AC=3x,$BC=\sqrt{7}x$,AB=2;
∴由余弦定理得:$cosC=\frac{2\sqrt{7}}{7}=\frac{9{x}^{2}+{7x}^{2}-4}{6\sqrt{7}{x}^{2}}$;
解得x=1,∴$AD=2,CB=\sqrt{7}$;
∴$\overrightarrow{AD}•\overrightarrow{CB}=2\sqrt{7}cos(π-C)$=$-2\sqrt{7}cosC=-2\sqrt{7}×\frac{2\sqrt{7}}{7}=-4$.
故答案为:-4.
点评 考查两角和的余弦公式,正余弦定理,以及数量积的计算公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
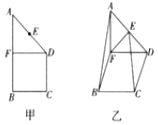 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的图象关于直线x=$\frac{π}{3}$对称 | |
| B. | f(x)的图象关于点($\frac{π}{4}$,0)对称 | |
| C. | 把f(x)的图象向左平移$\frac{π}{12}$个单位长度,得到一个偶函数的图象 | |
| D. | f(x)的最小正周期为π,且在[0,$\frac{π}{6}$]上为增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com