
【题目】已知正项数列{an}满足:a1=3,(2n﹣1)an+2=(2n+1)an﹣1+8n2(n>1,n∈N*),设 ![]() ,数列{bn}的前n项的和Sn , 则Sn的取值范围为( )
,数列{bn}的前n项的和Sn , 则Sn的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某学校有体育特长生25人,美术特长生35人,音乐特长生40人.用分层抽样的方法从中抽取40人,则抽取的体育特长生、美术特长生、音乐特长生的人数分别为( )
A.8,14,18
B.9,13,18
C.10,14,16
D.9,14,17
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)=sinx+ ![]() cosx(x∈R),先将y=f(x)的图象上所有点的横坐标缩短到原来的
cosx(x∈R),先将y=f(x)的图象上所有点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),再将得到的图象上所有点向右平行移动θ(θ>0)个单位长度,得到的图象关于直线x=
倍(纵坐标不变),再将得到的图象上所有点向右平行移动θ(θ>0)个单位长度,得到的图象关于直线x= ![]() 对称,则θ的最小值为( )
对称,则θ的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2C﹣3cos(A+B)=1
(1)求角C的大小;
(2)若c= ![]() ,求△ABC周长的最大值.
,求△ABC周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是圆柱底面圆周的四等分点,
是圆柱底面圆周的四等分点, ![]() 是圆心,
是圆心, ![]() ,
, ![]() ,
, ![]() 与底面
与底面![]() 垂直,底面圆的直径等于圆柱的高.
垂直,底面圆的直径等于圆柱的高.
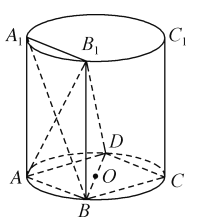
(1)证明: ![]() ;
;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 沿着三条中位线折起后能够拼接成一个三棱锥,则称这样的
沿着三条中位线折起后能够拼接成一个三棱锥,则称这样的![]() 为“和谐三角形”,设
为“和谐三角形”,设![]() 的三个内角分别为
的三个内角分别为![]() ,
, ![]() ,
, ![]() ,则下列条件不能够确定为“和谐三角形”的是
,则下列条件不能够确定为“和谐三角形”的是![]()
A. ![]() ; B.
; B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的不恒为零的函数,且对于任意实数x,y满足:f(2)=2,f(xy)=xf(y)+yf(x),an= ![]() (n∈N*),bn=
(n∈N*),bn= ![]() (n∈N*),考查下列结论:
(n∈N*),考查下列结论:
①f(1)=1;②f(x)为奇函数;③数列{an}为等差数列;④数列{bn}为等比数列.
以上命题正确的是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com