
����Ŀ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() ��
��
��1����ֱ��![]() ��ֱ��
��ֱ��![]() ƽ�У���ʵ��
ƽ�У���ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ��
�� ![]() ����
����![]() ��ֱ��
��ֱ��![]() �ϣ���֪
�ϣ���֪![]() ���е���
���е���![]() ���ϣ����
���ϣ����![]() �����꣮
�����꣮
���𰸡���1��![]() ����2��
����2��![]()
�������������������1��������ֱ��ƽ�У���Ӧ�����������ߣ��з��̼������![]() ��ֵ����2������
��ֵ����2������![]() ʱ��ֱ��
ʱ��ֱ��![]() �ķ��������
�ķ��������![]() �����꣬�ɴ����
�����꣬�ɴ����![]() ���е����꣬�����е���
���е����꣬�����е���![]() ���������
���������![]() ������.
������.
�����������1����ֱ��![]() ��ֱ��
��ֱ��![]() ƽ�У�
ƽ�У�
��![]() ��
��
��![]() ��������֪���������⣮
��������֪���������⣮
��2���������֪�� ![]() ��
��
��![]() ����
����![]() ���е�Ϊ
���е�Ϊ![]() ��
��
��![]() �����
���е���![]() ���ϣ���
���ϣ���![]() ��
��
��![]() ��
��
�����͡������
��������
16
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��ABC������������ΪA(7��8)��B(10��4)��C(2����4)��
(1)��BC���ϵ���������ֱ�ߵķ��̣�
(2)��BC���ϵĸ�����ֱ�ߵķ��̣�
���𰸡���1��![]() ����2��
����2��![]()
�������������������1�������е����깫ʽ���![]() �е�
�е�![]() �����꣬����б�ʹ�ʽ�����
�����꣬����б�ʹ�ʽ�����![]() ��б�ʣ����õ�бʽ����
��б�ʣ����õ�бʽ����![]() ���ϵ���������ֱ�ߵķ��̣���2���ȸ���б�ʹ�ʽ���
���ϵ���������ֱ�ߵķ��̣���2���ȸ���б�ʹ�ʽ���![]() ��б�ʣ��Ӷ����
��б�ʣ��Ӷ����![]() ���ϵĸ�����ֱ�ߵ�б��Ϊ
���ϵĸ�����ֱ�ߵ�б��Ϊ![]() �����õ�бʽ����
�����õ�бʽ����![]() ���ϵĸ�����ֱ�ߵķ���.
���ϵĸ�����ֱ�ߵķ���.
�����������1����B(10��4)��C(2����4)����BC�е�D������Ϊ��6��0����
����AD��б��Ϊk��![]() ��8��
��8��
����BC���ϵ�����AD����ֱ�ߵķ���Ϊy��0��8(x��6)��
��8x��y��48��0��
��2����B(10��4)��C(2����4)����BC����ֱ�ߵ�б��Ϊk��![]() ��1��
��1��
����BC���ϵĸ�����ֱ�ߵ�б��Ϊ��1��
����BC���ϵĸ�����ֱ�ߵķ���Ϊy��8����(x��7)����x��y��15��0��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=cosxsin��x+![]() ����
����![]() cos2x+
cos2x+![]() ��x��R��
��x��R��
��1����f��x���ĵ����������䣻
��2���������ABC�У���A��B��C�ĶԱ߷ֱ�a��b��c����f��A��=![]() ��a=
��a=![]() ������ABC��������ֵ��
������ABC��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
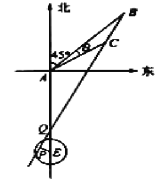
����Ŀ�� ��һ���ض�ʱ���ڣ��Ե�EΪ���ĵ�7�������ں�����Ϊ����ˮ��.��E����55���ﴦ��һ���״�۲�վA.ijʱ�̲��һ������ֱ����ʻ�Ĵ�ֻλ�ڵ�A��ƫ��![]() �����A���40
�����A���40![]() �����λ��B������40�����ֲ�øô�����ʻ����A��ƫ��
�����λ��B������40�����ֲ�øô�����ʻ����A��ƫ��![]() +
+![]() (����sin
(����sin![]() =
=![]() ��
��![]() )�����A���10
)�����A���10![]() ������C.
������C.
��I����ô�����ʻ�ٶȣ���λ������/Сʱ��;
��II�����ô����ı亽�з��������ʻ.�ж����Ƿ����뾯��ˮ��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������װ��5�ű������Ϊ1��2��3��4��5�Ŀ�Ƭ����5 �ſ�Ƭ����������ȫ��ͬ.�ֽ����зŻص�������ȡ2 �Σ�ÿ�������ȡ��һ�ſ�Ƭ.
��1��������п��ܽ���������г����п��ܽ����
��2�����¼���ȡ����Ƭ����֮�Ͳ�С��7 ��С��5���ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ��Բ
��Բ![]() ��
�� ![]() .
.
(1)��ֱ��![]() ����
����![]() ����Բ��
����Բ��![]() �ľ���Ϊ
�ľ���Ϊ![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
(2)��ֱ��![]() ��Բ
��Բ![]() ����
����![]() ��
�� ![]() ���㣬�Ƿ����ʵ��
���㣬�Ƿ����ʵ��![]() ��ʹ�ù���
��ʹ�ù���![]() ��ֱ��
��ֱ��![]() ��ֱƽ����
��ֱƽ����![]() �������ڣ����ʵ��
�������ڣ����ʵ��![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ٰ�У�Ƽ��Ļ������ڣ���ͬһʱ�䰲�š�����Ȥζ��ѧ���͡�У�赸������������������֪A��B��ѧϰС�����5λͬѧ��ÿλͬѧ��������������ѡ��һ������A��1��ѡ��������Ȥζ��ѧ��������4��ѡ����У�赸��������B��2��ѡ��������Ȥζ��ѧ��������3��ѡ����У�赸��������
��1�����Ӵ�10��������ѡ��3�ˣ���ѡ����3����ǡ��2��ѡ����У�赸�������ĸ��ʣ�
��2������A��B�����и���ѡ2�ˣ���XΪѡ����4����ѡ��������Ȥζ��ѧ������������X�ķֲ��к���ѧ����E��X����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}�ĸ����Ϊ������a1=1��ǰn���ΪSn �� ��an+12��n��2��1=2��Sn �� ��Ϊ��������
��1��������{an}��ͨ�ʽ��
��2����bn= ![]() ��Cn=
��Cn= ![]() +
+ ![]() ��k��n��N*��k��2n+2���� ��֤��
��k��n��N*��k��2n+2���� ��֤��
��bn��bn+1��
��Cn��Cn+1 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x����R�ϴ��ڵ���f�䣨x����x��R����f����x��+f��x��=x2 �� �ڣ�0��+�ޣ���f�䣨x����x����f��6��m����f��m����18+6m��0����ʵ��m��ȡֵ��ΧΪ�� ��
A.[��3��3]
B.[3��+�ޣ�
C.[2��+�ޣ�
D.�����ޣ���2]��[2��+�ޣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com