
【题目】将函数f(x)=cos(x+ ![]() )图象上所有点的横坐标缩短为原来的
)图象上所有点的横坐标缩短为原来的 ![]() 倍,纵坐标不变,得到函数g(x)的图象,则函数g(x)的一个减区间是( )
倍,纵坐标不变,得到函数g(x)的图象,则函数g(x)的一个减区间是( )
A.[﹣ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
【答案】D
【解析】解:将函数f(x)=cos(x+ ![]() )图象上所有点的横坐标缩短为原来的
)图象上所有点的横坐标缩短为原来的 ![]() 倍,纵坐标不变,
倍,纵坐标不变,
则y=cos(2x+ ![]() ),
),
即g(x)=cos(2x+ ![]() ),
),
由2kπ≤2x+ ![]() ≤2kπ+π,k∈Z,
≤2kπ+π,k∈Z,
得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
即函数的单调递减区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z,
],k∈Z,
当k=0时,单调递减区间为[﹣ ![]() ,
, ![]() ],
],
故选:D.
【考点精析】利用函数y=Asin(ωx+φ)的图象变换对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣ ![]() ax2 , 且关于x的方程f(x)+a=0有三个不等的实数根,则实数a的取值范围是( )
ax2 , 且关于x的方程f(x)+a=0有三个不等的实数根,则实数a的取值范围是( )
A.(﹣∞,﹣ ![]() )∪(0,
)∪(0, ![]() )
)
B.(﹣ ![]() ,0)∪(
,0)∪( ![]() ,+∞)
,+∞)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F. 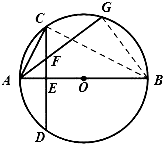
(1)求证:E、F、G、B四点共圆;
(2)若GF=2FA=4,求线段AC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,D是BC的中点. 
(1)若E为B1C1的中点,求证:BE∥平面AC1D;
(2)若平面B1BCC1⊥平面ABC,且AB=AC,求证:平面AC1D⊥平面B1BCC1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() +lnx,其中a为实常数.
+lnx,其中a为实常数.
(1)讨论f(x)的单调性;
(2)不等式f(x)≥1在x∈(0,1]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为 ![]() (θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(1)求C1和C2在直角坐标系下的普通方程;
(2)已知直线l:y=x和曲线C1交于M,N两点,求弦MN中点的极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com