
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,上下顶点分别为
,上下顶点分别为![]() ,
,![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,离心率为e.
,离心率为e.
(1)若![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,且
,且 ,求椭圆C的方程;
,求椭圆C的方程;
(2)若![]() ,设直线
,设直线![]() 与椭圆C相交于P,Q两点,
与椭圆C相交于P,Q两点,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,坐标原点O在以MN为直径的圆上,且
的中点,坐标原点O在以MN为直径的圆上,且![]() ,求实数k的取值范围.
,求实数k的取值范围.
科目:高中数学 来源: 题型:
【题目】东方商店欲购进某种食品(保质期两天),此商店每两天购进该食品一次(购进时,该食品为刚生产的).根据市场调查,该食品每份进价![]() 元,售价
元,售价![]() 元,如果两天内无法售出,则食品过期作废,且两天内的销售情况互不影响,为了了解市场的需求情况,现统计该产品在本地区
元,如果两天内无法售出,则食品过期作废,且两天内的销售情况互不影响,为了了解市场的需求情况,现统计该产品在本地区![]() 天的销售量如下表:
天的销售量如下表:

(视样本频率为概率)
(1)根据该产品![]() 天的销售量统计表,记两天中一共销售该食品份数为
天的销售量统计表,记两天中一共销售该食品份数为![]() ,求
,求![]() 的分布列与期望
的分布列与期望
(2)以两天内该产品所获得的利润期望为决策依据,东方商店一次性购进![]() 或
或![]() 份,哪一种得到的利润更大?
份,哪一种得到的利润更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 下列结论错误的是
A. 命题:“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”
”
B. “![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 命题:“![]() ,
, ![]() ”的否定是“
”的否定是“![]() ,
, ![]() ”
”
D. 若“![]() ”为假命题,则
”为假命题,则![]() 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,上下顶点分别为
,上下顶点分别为![]() ,
,![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,离心率为e.
,离心率为e.
(1)若![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,且
,且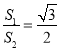 ,求椭圆C的方程;
,求椭圆C的方程;
(2)若![]() ,设直线
,设直线![]() 与椭圆C相交于P,Q两点,
与椭圆C相交于P,Q两点,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,坐标原点O在以MN为直径的圆上,且
的中点,坐标原点O在以MN为直径的圆上,且![]() ,求实数k的取值范围.
,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点
为参数),以直角坐标系的原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,求三条曲线
,求三条曲线![]() ,
,![]() ,
,![]() 所围成图形的面积.
所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】折纸与数学有着千丝万缕的联系,吸引了人们的广泛兴趣.因![]() 纸的长宽比
纸的长宽比![]() 称为白银分割比例,故
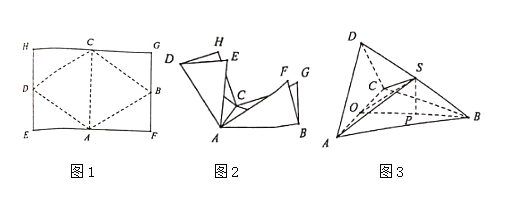
称为白银分割比例,故![]() 纸有一个白银矩形的美称.现有一张如图1所示的
纸有一个白银矩形的美称.现有一张如图1所示的![]() 纸
纸![]() ,
,![]() .
.
![]() 分别为
分别为![]() 的中点,将其按折痕
的中点,将其按折痕![]() 折起(如图2),使得
折起(如图2),使得![]() 四点重合,重合后的点记为
四点重合,重合后的点记为![]() ,折得到一个如图3所示的三棱锥
,折得到一个如图3所示的三棱锥![]() .记
.记![]() 为
为![]() 的中点,在
的中点,在![]() 中,
中,![]() 为
为![]() 边上的高.
边上的高.
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 分别是棱
分别是棱![]() 上的动点,且
上的动点,且![]() .当三棱锥
.当三棱锥![]() 的体积最大时,求平面
的体积最大时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.

(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com