
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 上一点
上一点![]() 处的切线
处的切线![]() 分别交
分别交![]() 轴
轴![]() 轴于点
轴于点![]() ,以
,以![]() 为顶点且以
为顶点且以![]() 为中心的椭圆记作
为中心的椭圆记作![]() ,直线
,直线![]() 交
交![]() 于
于![]() 两点.
两点.
(1)若椭圆![]() 的离心率为
的离心率为![]() ,求
,求![]() 点坐标;
点坐标;
(2)证明:四边形![]() 的面积
的面积![]() .
.
【答案】(1)![]() .(2)证明见解析
.(2)证明见解析
【解析】
(1)由切线得![]() ,写出直线
,写出直线![]() 方程,求出
方程,求出![]() 两点坐标,得椭圆标准方程,然后分类讨论求椭圆的离心率,由离心率是
两点坐标,得椭圆标准方程,然后分类讨论求椭圆的离心率,由离心率是![]() 求得
求得![]() 点坐标;
点坐标;
(2)设![]() 方程为
方程为![]() (
(![]() 且
且![]() ),由此写出切线
),由此写出切线![]() 方程求得
方程求得![]() 坐标,得椭圆方程,由直线
坐标,得椭圆方程,由直线![]() 方程与椭圆方程联立可得
方程与椭圆方程联立可得![]() 点坐标,求出
点坐标,求出![]() ,再求出
,再求出![]() ,由对称性可得
,由对称性可得![]() ,注意计算时
,注意计算时![]() ,令
,令![]() (
(![]() )换元,然后利用基本不等式和函数性质可证得结论.
)换元,然后利用基本不等式和函数性质可证得结论.
(1)依题意![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得![]() ,
,
令![]() 得
得![]() ,
,
∴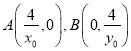 ,
,
椭圆![]() 的方程为
的方程为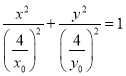 .
.
(1)若![]() ,
,
则椭圆的离心率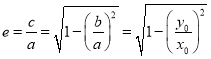 ,由
,由![]() 得
得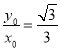 ,而
,而![]() ,
,
∴![]() ,则点
,则点![]() ;
;
(2)若![]() ,同理可得点
,同理可得点![]() ,
,
综上可得![]() 点坐标为
点坐标为![]() 或
或![]() .
.
(2)证明:直线![]() 的斜率为
的斜率为![]() ,依题意有
,依题意有![]() 且
且![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得![]() ,令
,令![]() 得
得![]() ,
,
∴![]() ,
,
椭圆![]() 的方程为
的方程为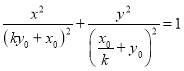 ,
,
联立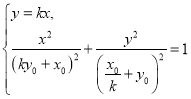 ,解得
,解得
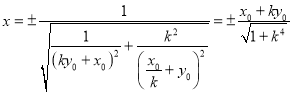 ,
,
∴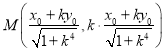 ,
,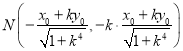 ,
,
![]()
![]()
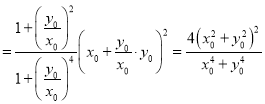
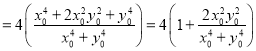
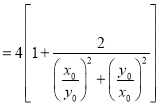
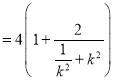
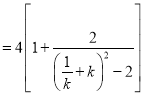 ,
,
∴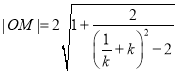 ,
,
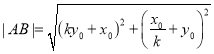
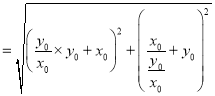
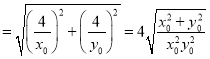
![]()
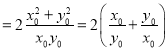
![]() ,
,
设![]() ,
,
![]()
![]() ,
,
设![]() ,
,
则![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
∴![]() ,∴
,∴![]() .
.


科目:高中数学 来源: 题型:
【题目】杭州西溪国家湿地公园是以水为主题的公园,以湿地良好生态环境和多样化湿地景观资源为基础的生态型主题公园.欲在该公园内搭建一个平面凸四边形![]() 的休闲观光及科普宣教的平台,如图所示,其中
的休闲观光及科普宣教的平台,如图所示,其中![]() 百米,
百米,![]() 百米,
百米,![]() 为正三角形.建成后
为正三角形.建成后![]() 将作为人们旅游观光休闲娱乐的区域,
将作为人们旅游观光休闲娱乐的区域,![]() 将作为科普宣教湿地功能利用弘扬湿地文化的区域.
将作为科普宣教湿地功能利用弘扬湿地文化的区域.
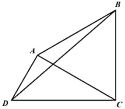
(1)当![]() 时,求旅游观光休闲娱乐的区域
时,求旅游观光休闲娱乐的区域![]() 的面积;
的面积;
(2)求旅游观光休闲娱乐的区域![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在1,2,3,4,5,6这六个数字所组成的允许有重复数字的三位数中,各个数位上的数字之和为9的三位数共有( )
A.16个B.18个C.24个D.25个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受突如其来的新冠疫情的影响,全国各地学校都推迟2020年的春季开学.某学校“停课不停学”,利用云课平台提供免费线上课程.该学校为了解学生对线上课程的满意程度,随机抽取了500名学生对该线上课程评分.其频率分布直方图如下:若根据频率分布直方图得到的评分低于80分的概率估计值为0.45.
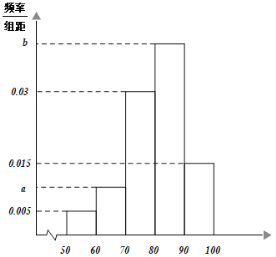
(1)(i)求直方图中的a,b值;
(ii)若评分的平均值和众数均不低于80分视为满意,判断该校学生对线上课程是否满意?并说明理由(同一组中的数据用该组区间的中点值为代表);
(2)若采用分层抽样的方法,从样本评分在[60,70)和[90,100]内的学生中共抽取5人进行测试来检验他们的网课学习效果,再从中选取2人进行跟踪分析,求这2人中至少一人评分在[60,70)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与椭圆
与椭圆![]() 有一个相同的焦点,过点
有一个相同的焦点,过点![]() 且与
且与![]() 轴不垂直的直线
轴不垂直的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)试问直线![]() 是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过焦点且垂直于
.过焦点且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 相交所得的弦长为3,直线
相交所得的弦长为3,直线![]() 与椭圆
与椭圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,问直线
,问直线![]() 是否存在?若存在,求直线
是否存在?若存在,求直线![]() 的斜率
的斜率![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,且
为平行四边形,且![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为60°,求平面
所成角为60°,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com