
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)经过点(0,
=1(a>b>0)经过点(0, ![]() ),离心率e=
),离心率e= ![]() .
.
(Ⅰ)求椭圆C的方程及焦距.
(Ⅱ)椭圆C的左焦点为F1 , 右顶点为A,经过点A的直线l与椭圆C的另一交点为P.若点B是直线x=2上异于点A的一个动点,且直线BF1⊥l,问:直线BP是否经过定点?若是,求出该定点的坐标;若不是,说明理由.
【答案】解:(I)由题意可得:b= ![]() ,
, ![]() ,a2=b2+c2 .
,a2=b2+c2 .
联立解得:a=2,c=1.
∴椭圆C的方程为: ![]() =1,焦距为2.
=1,焦距为2.
(II)设PA的方程为:my=x﹣2.(m≠0).
联立 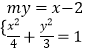 ,化为:(3m2+4)y2+12my=0,
,化为:(3m2+4)y2+12my=0,
解得yP= ![]() ,∴xP=
,∴xP= ![]() .
.
∴P ![]() .
.
设B(2,t),则 ![]() =﹣1,解得t=﹣3m.
=﹣1,解得t=﹣3m.
∴直线BP的方程为:y+3m= 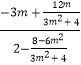 (x﹣2),
(x﹣2),
化为:4y+m(6+3x)=0,令6+3x=0,4y=0,
解得x=﹣2,y=0.
∴直线BP经过定点(﹣2,0).
【解析】(I)由题意可得:b= ![]() ,
, ![]() ,a2=b2+c2 . 联立解得:a,c.即可得出椭圆C的方程及其焦距.(II)设PA的方程为:my=x﹣2.(m≠0).与椭圆方程联立化为:(3m2+4)y2+12my=0,
,a2=b2+c2 . 联立解得:a,c.即可得出椭圆C的方程及其焦距.(II)设PA的方程为:my=x﹣2.(m≠0).与椭圆方程联立化为:(3m2+4)y2+12my=0,
解得P ![]() .设B(2,t),根据
.设B(2,t),根据 ![]() =﹣1,解得t=﹣3m.可得直线BP的方程为:y+3m=kBP(x﹣2),可得直线BP经过定点(﹣2,0).
=﹣1,解得t=﹣3m.可得直线BP的方程为:y+3m=kBP(x﹣2),可得直线BP经过定点(﹣2,0).


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某零售店近5个月的销售额和利润额资料如下表:
商店名称 |
|
|
|
|
|
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额![]() 关于销售额
关于销售额![]() 的回归直线方程;
的回归直线方程;
(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).
[参考公式: ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过右焦点F2(c,0)垂直于x轴的直线与椭圆交于A,B两点且|AB|=
,过右焦点F2(c,0)垂直于x轴的直线与椭圆交于A,B两点且|AB|= ![]() ,又过左焦点F1(﹣c,0)任作直线l交椭圆于点M
,又过左焦点F1(﹣c,0)任作直线l交椭圆于点M
(1)求椭圆C的方程
(2)椭圆C上两点A,B关于直线l对称,求△AOB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】min(a,b)表示a,b中的最小值,执行如图所示的程序框图,若输入的a,b值分别为4,10,则输出的min(a,b)值是( ) 
A.0
B.1
C.2
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P1(x1 , y1),P2(x2 , y2),P3(x3 , y3),P4(x4 , y4),P5(x5 , y5),P6(x6 , y6)是抛物线C:y2=2px(p>0)上的点,F是抛物线C的焦点,若|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|=36,且x1+x2+x3+x4+x5+x6=24,则抛物线C的方程为( )
A.y2=4x
B.y2=8x
C.y2=12x
D.y2=16x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() :
:![]() .
.

(Ⅰ)若圆C与x轴相切,求圆C的方程;
(Ⅱ)已知![]() ,圆
,圆![]() 与x轴相交于两点
与x轴相交于两点![]() (点
(点![]() 在点
在点![]() 的左侧).过点
的左侧).过点![]() 任作一条直线与圆
任作一条直线与圆![]() :
:![]() 相交于两点A,B.问:是否存在实数a,使得
相交于两点A,B.问:是否存在实数a,使得![]() =
=![]() ?若存在,求出实数a的值,若不存在,请说明理由.
?若存在,求出实数a的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为 ![]() (φ为参数),以原点为极点,x轴的非负半轴为极轴建立极坐标系. (Ⅰ)求曲线C的极坐标方程;
(φ为参数),以原点为极点,x轴的非负半轴为极轴建立极坐标系. (Ⅰ)求曲线C的极坐标方程;
(Ⅱ)已知倾斜角为135°且过点P(1,2)的直线l与曲线C交于M,N两点,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com