
| A. | $({\frac{1}{3},\frac{1}{2}})$ | B. | $({\frac{1}{3},\frac{1}{2}})∪({1,+∞})$ | C. | (1,+∞) | D. | $({\frac{1}{3},1})∪({1,+∞})$ |
分析 当a>1时,由题意可得3a-1>a解得实数a的取值范围.当0<a<1时,由题意可得0<3a-1<a,解得实数a的取值范围.再把这两个当a的取值范围取并集,即得所求.
解答 解:当a>1时,由loga(3a-1)>1可得3a-1>a,解得a>$\frac{1}{2}$,故实数a的取值范围为(1,+∞).
当0<a<1时,由loga(3a-1)>1可得0<3a-1<a,解得$\frac{1}{3}$<a<$\frac{1}{2}$,故实数a的取值范围为($\frac{1}{3}$,$\frac{1}{2}$).
综上可得,所求的实数a的取值范围为(1,+∞)∪($\frac{1}{3}$,$\frac{1}{2}$),
故选B.
点评 本题主要考查对数不等式的解法,体现了分类讨论的数学思想,属于中档题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.08 |
| x+3 | 2 | 3 | 4 | 5 | 6 |
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 54 | B. | 108 | C. | 162 | D. | 324 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
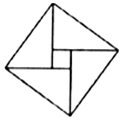 第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.
第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com