
【题目】(理)已知数列![]() 满足
满足![]() (
(![]() ),首项
),首项![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)数列![]() 满足
满足![]() ,记数列
,记数列 的前
的前![]() 项和为
项和为![]() ,
,![]() 是△ABC的内角,若
是△ABC的内角,若![]() 对于任意
对于任意![]() 恒成立,求角
恒成立,求角![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知直线![]() 是双曲线
是双曲线![]() 的一条渐近线,点
的一条渐近线,点![]() 在双曲线C上,设坐标原点为O.
在双曲线C上,设坐标原点为O.
(1)求双曲线C的方程;
(2)若过点![]() 的直线l与双曲线C交于R、S两点,若
的直线l与双曲线C交于R、S两点,若![]() ,求直线l的方程;
,求直线l的方程;
(3)设![]() 在双曲线上,且直线AM与y轴相交于点P,点M关于y轴对称的点为N,直线AN与y轴相交于点Q,问:在x轴上是否存在定点T,使得
在双曲线上,且直线AM与y轴相交于点P,点M关于y轴对称的点为N,直线AN与y轴相交于点Q,问:在x轴上是否存在定点T,使得![]() ?若存在,求出点T的坐标;若不存在,说明理由.
?若存在,求出点T的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
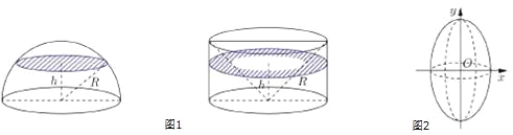
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() 的方程为
的方程为![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴正半轴建立直角坐标系
轴正半轴建立直角坐标系![]() .
.
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与曲线
,与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)![]() 是函数数
是函数数![]() 的导函数,记
的导函数,记![]() ,若
,若![]() 在区间
在区间![]() 上为单调函数,求实数a的取值范围;
上为单调函数,求实数a的取值范围;
(2)设实数![]() ,求证:对任意实数
,求证:对任意实数![]()
![]() ,总有
,总有![]() 成立.
成立.
附:简单复合函数求导法则为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
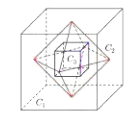
【题目】如图,记棱长为1的正方体![]() ,以
,以![]() 各个面的中心为顶点的正八面体为
各个面的中心为顶点的正八面体为![]() ,以
,以![]() 各面的中心为顶点的正方体为
各面的中心为顶点的正方体为![]() ,以
,以![]() 各个面的中心为顶点的正八面体为
各个面的中心为顶点的正八面体为![]() ,……,以此类推得一系列的多面体
,……,以此类推得一系列的多面体![]() ,设
,设![]() 的棱长为
的棱长为![]() ,则数列
,则数列![]() 的各项和为________.
的各项和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,并且
,并且![]() ,
,![]() ,数列
,数列![]() 满足:
满足:![]() ,
,![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和公式
项和公式![]() ;
;
(2)求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和公式
项和公式![]() ;
;
(3)记集合![]() ,若
,若![]() 的子集个数为16,求实数
的子集个数为16,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
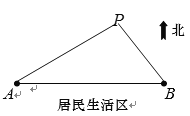
【题目】如图所示,![]() 、
、![]() 是两个垃圾中转站,
是两个垃圾中转站,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处,
千米处,![]() 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在
的南面为居民生活区.为了妥善处理生活垃圾,政府决定在![]() 的北面建一个垃圾发电厂
的北面建一个垃圾发电厂![]() .垃圾发电厂
.垃圾发电厂![]() 的选址拟满足以下两个要求(
的选址拟满足以下两个要求(![]() 、
、![]() 、
、![]() 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点
可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点![]() 到直线
到直线![]() 的距离要尽可能大).现估测得
的距离要尽可能大).现估测得![]() 、
、![]() 两个中转站每天集中的生活垃圾量分别约为
两个中转站每天集中的生活垃圾量分别约为![]() 吨和
吨和![]() 吨.设
吨.设![]() .
.
(1)求![]() (用
(用![]() 的表达式表示);
的表达式表示);
(2)垃圾发电厂该如何选址才能同时满足上述要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的颗粒物,也称为可入肺颗粒物.虽然
微米的颗粒物,也称为可入肺颗粒物.虽然![]() 只是地球大气成分中含量很少的组分,但它对空气质量和能见度等有重要的影响.我国
只是地球大气成分中含量很少的组分,但它对空气质量和能见度等有重要的影响.我国![]() 标准如下表所示.我市环保局从市区四个监测点2018年全年每天的
标准如下表所示.我市环保局从市区四个监测点2018年全年每天的![]() 监测数据中随机抽取
监测数据中随机抽取![]() 天的数据作为样本,监测值如茎叶图如图所示.
天的数据作为样本,监测值如茎叶图如图所示.
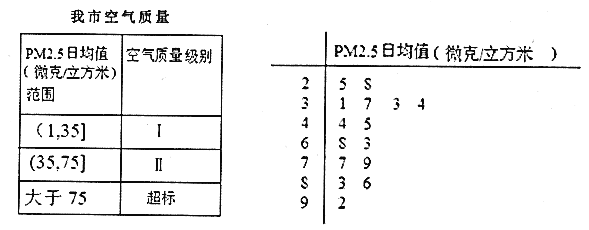
(Ⅰ)求这![]() 天数据的平均值;
天数据的平均值;
(Ⅱ)从这![]() 天的数据中任取
天的数据中任取![]() 天的数据,记表示其中空气质量达到一级的天数
天的数据,记表示其中空气质量达到一级的天数![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)以![]() 天的
天的![]() 日均值来估计一年的空气质量情况,则一年(按
日均值来估计一年的空气质量情况,则一年(按![]() 天计算)中大约有多少天的空气质量达到一级.
天计算)中大约有多少天的空气质量达到一级.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com