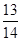设等差数列{
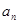
}{
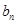
}的前n 项和为
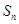
,
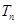
,若
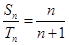
,则
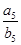
=
试题分析:依据等差数列求和公式可得

点评:等差数列性质:若

则
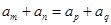
,求和公式

,本题是求和公式的反用,学生不易想到
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知数列

中,

,满足

。
(1)求证:数列

为等差数列;
(2)求数列

的前

项和

.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知数列
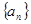
中, a
2=7,且a
n =a
n+1-6(n∈
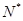
),则前n项和S
n=" (" )
A.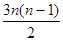 | B. n2 | C.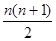 | D.3n2 –2n |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(1)已知数列
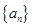
的前
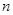
项和为
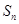
,
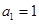
,
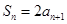
,求
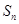
(2)已知等差数列
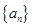
的前
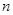
项和为
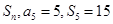
,求数列
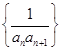
的前2012项和
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设等差数列
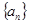
的前
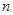
项和为
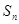
,已知

,
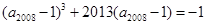
,则下列结论中正确的是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设等差数列
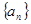
的前
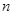
项和为
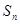
,若
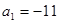
,
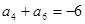
,则当
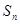
取最小值时,
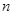
等于( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设数列
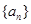
的前
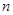
项和为
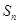
,
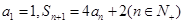
.
(1)若
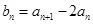
,求
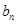
;
(2)若
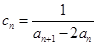
,求
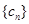
的前6项和
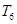
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
等差数列
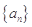
中,
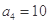
且
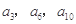
成等比数列,
(1)求数列
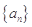
的通项公式; (2)求前20项的和
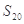
。
查看答案和解析>>

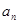 }{
}{ 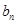 }的前n 项和为
}的前n 项和为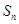 ,
,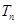 ,若
,若 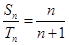 ,则
,则 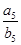 =
=