
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M,N分别是最大、最小值点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0,则A=$\frac{π}{6}$.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M,N分别是最大、最小值点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0,则A=$\frac{π}{6}$. 分析 由题意写出点M、N的坐标,利用$\overrightarrow{OM}$•$\overrightarrow{ON}$=0,即可求出A的值.
解答  解:由题意,M,N分别是这段图象的最高点和最低点,O为坐标原点,
解:由题意,M,N分别是这段图象的最高点和最低点,O为坐标原点,
∴$\overrightarrow{OM}$=($\frac{π}{12}$,A),$\overrightarrow{ON}$=($\frac{π}{3}$,-A),
则$\overrightarrow{OM}$•$\overrightarrow{ON}$=$\frac{π}{12}$×$\frac{π}{3}$-A2=0,
解得A=$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题考查三角函数的图象与应用问题,也考查了平面向量数量积的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | c<b<a | C. | b<c<a | D. | a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,从图中可以得到这10位同学身高的中位数是( )
如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,从图中可以得到这10位同学身高的中位数是( )| A. | 161 cm | B. | 162 cm | C. | 163 cm | D. | 164 cm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
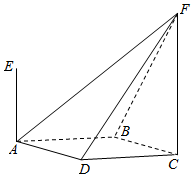 如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$,AE、CF都与平面ABCD垂直,AE=1,CF=2.
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$,AE、CF都与平面ABCD垂直,AE=1,CF=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com