
分析 由{x,$\frac{y}{|x|}$,0}={x-3,-$\frac{x}{|y|}$,3}可得B={0,-1,3};化简可得A={-1,3};从而证明.
解答 证明:∵{x,$\frac{y}{|x|}$,0}={x-3,-$\frac{x}{|y|}$,3},
∴x-3=0,即x=3,
∴{3,$\frac{y}{3}$,0}={0,-$\frac{3}{|y|}$,3},
∴$\frac{y}{3}$=-$\frac{3}{|y|}$,
∴y=-3,
故B={0,-1,3};
①当a>0,b>0时,y=$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{ab}{|ab|}$=3;
②当a>0,b<0时,y=$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{ab}{|ab|}$=-1;
③当a<0,b>0时,y=$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{ab}{|ab|}$=-1;
④当a<0,b<0时,y=$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{ab}{|ab|}$=-1;
故A={-1,3};
故A$\frac{?}{≠}$B.
点评 本题考查了集合的化简与应用.


科目:高中数学 来源: 题型:解答题
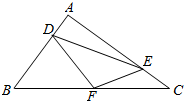 在△ABC中,AB⊥AC,AB=3,AC=4,D,E分别是边AB,AC上的点,且AD=CE=x,设四边形BDEC的面积为S,周长为c.
在△ABC中,AB⊥AC,AB=3,AC=4,D,E分别是边AB,AC上的点,且AD=CE=x,设四边形BDEC的面积为S,周长为c.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | -10 | C. | $\frac{1}{10}$ | D. | -$\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点A在半径为1且圆心在原点的圆上,∠A0x=45°,点P从点A出发,依逆时针方向匀速地沿单位圆周旋转.已知P在1s内转过的角度为θ(0°<θ<180°),经过2s到达第三象限,经过14s后又回到出发点A.求θ,并判断其所在的象限.
如图,点A在半径为1且圆心在原点的圆上,∠A0x=45°,点P从点A出发,依逆时针方向匀速地沿单位圆周旋转.已知P在1s内转过的角度为θ(0°<θ<180°),经过2s到达第三象限,经过14s后又回到出发点A.求θ,并判断其所在的象限.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com