
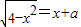 有两个不相等的实根,则a的取值范围是 .
有两个不相等的实根,则a的取值范围是 . 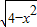 ,为圆心为坐标原点,半径为2的半圆,根据题意画出图形,当直线与半圆相切时,圆心到直线的距离d=r,利用点到直线的距离公式列出关于a的方程,求出此时a的值;当直线过(2,0)时,把此点坐标代入直线方程求出此时a的值,方程有两个不相等的实根即为两函数图形有两个交点,故根据求出的两种情况a的值写出满足题意的a的范围即可.
,为圆心为坐标原点,半径为2的半圆,根据题意画出图形,当直线与半圆相切时,圆心到直线的距离d=r,利用点到直线的距离公式列出关于a的方程,求出此时a的值;当直线过(2,0)时,把此点坐标代入直线方程求出此时a的值,方程有两个不相等的实根即为两函数图形有两个交点,故根据求出的两种情况a的值写出满足题意的a的范围即可.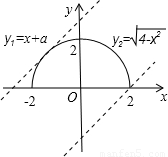
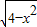 ,
,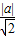 =2,
=2,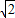 或a=-2
或a=-2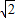 (舍去),
(舍去),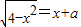 有两个不相等的实根,
有两个不相等的实根,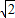 ).
).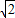 )
)

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
(09年宜昌一中12月月考理)(14分)
已知二次函数![]() 。
。
(1)若对任意x1,x2∈R,且![]() ,都有
,都有![]() ,求证:关于x的方程
,求证:关于x的方程![]() 有两个不相等的实数根且必有一个根属于(
有两个不相等的实数根且必有一个根属于(![]() );
);
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二次函数![]() 。
。
(1)若任意x1,x2∈R,且![]() ,都有
,都有![]() ,求证:关于x的方程
,求证:关于x的方程![]() 有两个不相等的实数根且必有一个根属于(
有两个不相等的实数根且必有一个根属于(![]() );
);
(2)若关于x的方程![]() 在(
在(![]() )的根为m,且
)的根为m,且![]() 成等差数列,设函数f (x)的图象的对称轴方程为
成等差数列,设函数f (x)的图象的对称轴方程为![]() ,求证:
,求证:![]() 。
。
查看答案和解析>>
科目:高中数学 来源:2015届浙江省绍兴市高一上学期阶段性考试数学试卷(解析版) 题型:选择题
若关于x的方程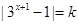 有两个不相等的实根,则实数
有两个不相等的实根,则实数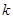 的取值范围是 ( )
的取值范围是 ( )
A.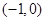 B.
B.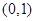 C.
C.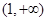 D.
D. 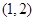
查看答案和解析>>
科目:高中数学 来源:2012届山东省高二上学期学业水平测试数学试卷 题型:解答题
已知命题p:关于x的方程 有两个不相等的负根. 命题q:关于x的方程
有两个不相等的负根. 命题q:关于x的方程
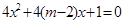 无实根,若
无实根,若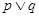 为真,
为真,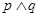 为假,求
为假,求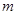 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com