
【题目】已知 ![]() :方程
:方程 ![]() 有两个不等的正根;
有两个不等的正根; ![]() :方程
:方程 ![]() 表示焦点在
表示焦点在 ![]() 轴上的双曲线.
轴上的双曲线.
(1)若 ![]() 为真命题,求实数
为真命题,求实数 ![]() 的取值范围;
的取值范围;
(2)若“ ![]() 或
或 ![]() ”为真,“
”为真,“ ![]() 且
且 ![]() ”为假,求实数
”为假,求实数 ![]() 的取值范围
的取值范围
【答案】
(1)解:由已知方程 ![]() 表示焦点在
表示焦点在 ![]() 轴上的双曲线,
轴上的双曲线,
所以 ![]() ,解得
,解得 ![]() ,即
,即 ![]()
(2)解:若方程 ![]() 有两个不等的正根,
有两个不等的正根,
则 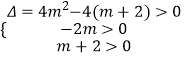 解得
解得 ![]() ,即
,即 ![]() .
.
因 ![]() 或
或 ![]() 为真,所以
为真,所以 ![]() 至少有一个为真.
至少有一个为真.
又 ![]() 且
且 ![]() 为假,所以
为假,所以 ![]() 至少有一个为假.
至少有一个为假.
因此, ![]() 两命题应一真一假,当
两命题应一真一假,当 ![]() 为真,
为真, ![]() 为假时,
为假时, ![]() ,解得
,解得 ![]() ;
;
当 ![]() 为假,
为假, ![]() 为真时,
为真时, ![]() ,解得
,解得 ![]() .
.
综上, ![]() 或
或 ![]() .
.
【解析】(1)根据题意结合已知条件焦点在 y 轴上的双曲线,即可得出关于m的不等式组解出m的取值范围即可。(2)利用题中条件当命题p为真命题时,借助二次函数根的情况以及韦达定理求出m的取值范围,结合题意由“ p 或 q ”为真,“ p 且 q ”为假可得出p 或 q 为真,所以 p 、 q 至少有一个为真.又 ![]() 且
且 ![]() 为假,所以
为假,所以 ![]() 至少有一个为假,按照这两种情况分情况讨论即可的出m的取值范围。
至少有一个为假,按照这两种情况分情况讨论即可的出m的取值范围。
【考点精析】通过灵活运用命题的真假判断与应用,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系即可以解答此题.


 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为 ![]() +
+ ![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线 ![]() ﹣
﹣ ![]() =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 ![]() .
.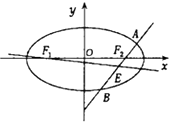
(1)求椭圆C的方程;
(2)设F1 , F2分别为椭圆C的左,右焦点,过F2作直线l(与x轴不重合)交于椭圆于A,B两点,线段AB的中点为E,记直线F1E的斜率为k,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有六间不同的电脑室,每天晚上至少开放两间,欲求不同安排方案的种数,现有3位同学分别给出了下列三个结果:① ![]() ;②26-7;③
;②26-7;③ ![]() ,其中正确的结论是( )
,其中正确的结论是( )
A.仅有①
B.仅有②
C.②与③
D.仅有③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表: 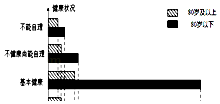
(1)若采取分层抽样的方法再从样本中的不能自理的老人中抽取16人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发 放生活补贴,标准如下:①80岁及以上长者每人每月发放生活补贴200元;②80岁以下 老人每人每月发放生活补贴120元;③不能自理的老人每人每月额外发放生活补贴100 元.试估计政府执行此计划的年度预算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正四面体的“骰子”(四个面分别标有1,2,3,4四个数字),掷一次“骰子”三个侧面的数字的和为“点数”,连续抛掷“骰子”两次.
(1)设A为事件“两次掷‘骰子’的点数和为16”,求事件A发生的概率;
(2)设X为两次掷“骰子”的点数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com