
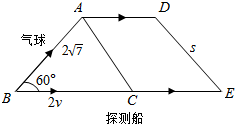
 在以v千米/小时的速度向东航行的科学探测船上释放了一个探测热气球,气球顺风与船同向,以2千米/小时的速度沿与水平方向成60°直线方向向上飘去,2小时后测得探测船与气球的距离为2$\sqrt{7}$千米,之后热气球沿水平方向仍以2千米/小时的速度飞行1小时,第二次测得探测船与热气球的距离为s千米.如图.
在以v千米/小时的速度向东航行的科学探测船上释放了一个探测热气球,气球顺风与船同向,以2千米/小时的速度沿与水平方向成60°直线方向向上飘去,2小时后测得探测船与气球的距离为2$\sqrt{7}$千米,之后热气球沿水平方向仍以2千米/小时的速度飞行1小时,第二次测得探测船与热气球的距离为s千米.如图.分析 (1)利用余弦定理解三角形ABC,得到关于v的等式解之;
(2)过C作直线DF⊥BE,垂足为F,得到DF,EF的长度,利用勾股定理得到s,得到所求.
解答 解:(1)在△ABC中,AB=2×2=4km,BC=2v,AC=2$\sqrt{7}$,∠ABC=60°,由余弦定理得到AC2=AB2+BC2-2AB×BCcos∠ABC,即28=16+4v2-8v,解得v=3,(v=-1舍去);
(2)过D作直线DF⊥BE,垂足为F,则DF=ABsin∠ABC=2$\sqrt{3}$km,EF=BE-BF=BE-ABcos∠ABC-AD=5km,
所以s=$\sqrt{D{F}^{2}+E{F}^{2}}$=$\sqrt{12+25}=\sqrt{37}$km,所以sin∠E=$\frac{DF}{s}$=$\frac{2\sqrt{3}}{\sqrt{37}}=\frac{3\sqrt{111}}{37}$.
所以第二次测距离时,从探测船位置观察热气球时仰角的正弦值为$\frac{3\sqrt{111}}{37}$.
点评 本题考查了解三角形;用到了余弦定理、勾股定理等知识.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{\sqrt{3}}{6}$,+∞) | B. | (0,e21) | C. | (e-11,e) | D. | (0,e11) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x-x2 | B. | y=|x+1| | C. | y=-$\frac{1}{x}$ | D. | y=x2-2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com