
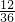 =
= .
.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:学习周报 数学 人教课标高二版(A必修5) 2009-2010学年 第13期 总第169期 人教课标版(A必修5) 题型:022
将甲、乙两枚骰子先后各抛一次,a、b分别表示抛掷甲、乙两枚骰子的点数.若点P(a,b)落在不等式组![]() 表示的平面区域内的事件记为A,则事件A的概率为________.
表示的平面区域内的事件记为A,则事件A的概率为________.
查看答案和解析>>
科目:高中数学 来源:全优设计必修三数学苏教版 苏教版 题型:044
将甲、乙两枚骰子先后各抛一次,a、b分别表示抛掷甲、乙两枚骰子所出的点数,若把点P(a,b)落在不等式组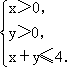 所表示的平面区域的事件记为A,求P(A).
所表示的平面区域的事件记为A,求P(A).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com