练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    解答题

    已知△ABC的三个顶点都在抛物线y2＝32x上，若A(2，8)，且三角形的重心与抛物线的焦点重合，求直线BC的方程．

    答案：
    解析：

    　　设B(x1，y1)、C(x2，y2)，抛物线焦点为(8，0)，由重心坐标公式

    　　得

    　　又＝＝－4，∴k＝－4．

    　　∴直线BC方程为y＋4＝－4(x－11)，即4x＋y－40＝0．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：中学教材标准学案　数学　高二上册 题型：044

    解答题

    已知△ABC的一条内角平分线CD的方程为2x＋y－1＝0，两个顶点A(1，2)，B(－1，－1)，求第三个顶点C的坐标．

    查看答案和解析>>

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    已知△ABC中，∠A、∠B、∠C的对边分别是a、b、c，若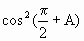＋cosA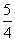＝，b＋c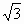＝a，求A、B、C的大小．

    查看答案和解析>>

    科目：高中数学 来源：2004年高考教材全程总复习试卷·数学 题型：044

    已知△ABC中∠A，∠B，∠C的对边分别为a，b，c且c＝10，若S△ABC＝9cot．

    (1)求|a－b|的值．

    (2)记O为AB的中点，求∠BOC的范围．

    查看答案和解析>>

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    已知△ABC中，A、B、C分别是三个内角，a、b、c分别是角A、B、C的对边，已知2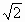(sin2A－sin2C)＝(a－b)sinB，△ABC的外接圆的半径为．

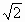    (Ⅰ)求角C；

    (Ⅱ)求△ABC面积S的最大值．

    查看答案和解析>>

    同步练习册答案