
【题目】设函数 ![]()
(1)若b和c分别是先后抛掷一枚骰子得到的点数,求对任意x∈R,f(x)>0恒成立的概率.
(2)若b是从区间[0,8](3)任取得一个数,c是从[0,6]任取的一个数,求函数f(x)的图象与x轴有交点的概率.
【答案】
(1)解:由点(b,c)组成的点共36tkh,
设A={任意x∈R,f(x)>0恒成立}即△=b2﹣c2<0,
∴b<c,A中包含基本事件15个,
∴P(A)= ![]() ;
;
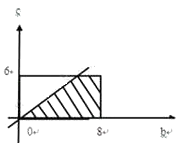
(2)解:(b,c)所在的区域Ω={(b,c)|0≤b≤8,0≤c≤6}
若使函数f(x)的图象与x轴有交点,
则b≥c≥0.
∴事件B={(b,c)|b>c,0≤b≤8,0≤c≤6}如图,
∴P(B)= ![]() .
.
【解析】(1)本题是一个等可能事件的概率,试验发生包含的事件数是6×6=36种结果,f(x)>0要满足判别式小于0,列举出结果.(2)利用几何概型的计算概率的方法解决本题,关键要弄准所求的随机事件发生的区域的面积和事件总体的区域面积,通过相除的方法完成本题的解答.
【考点精析】通过灵活运用几何概型,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等即可以解答此题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】己知函数f(x)=sinx+ ![]() cosx(x∈R),先将y=f(x)的图象上所有点的横坐标缩短到原来的
cosx(x∈R),先将y=f(x)的图象上所有点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),再将得到的图象上所有点向右平行移动θ(θ>0)个单位长度,得到的图象关于直线x=
倍(纵坐标不变),再将得到的图象上所有点向右平行移动θ(θ>0)个单位长度,得到的图象关于直线x= ![]() 对称,则θ的最小值为( )
对称,则θ的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 沿着三条中位线折起后能够拼接成一个三棱锥,则称这样的
沿着三条中位线折起后能够拼接成一个三棱锥,则称这样的![]() 为“和谐三角形”,设
为“和谐三角形”,设![]() 的三个内角分别为
的三个内角分别为![]() ,
, ![]() ,
, ![]() ,则下列条件不能够确定为“和谐三角形”的是
,则下列条件不能够确定为“和谐三角形”的是![]()
A. ![]() ; B.
; B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,200),[220.240),
[240,260),[260,280),[280,300)分组的频率分布直方图如图.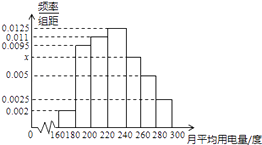
(1)求直方图中x的值;
(2)在月平均用电量为,[220,240),[240,260),[260,280)的三用户中,用分层抽样的方法抽取10居民,则月平均用电量在[220,240)的用户中应抽取多少户?
(3)求月平均用电量的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +
+ ![]() =1(a>b>0)过点A(1,
=1(a>b>0)过点A(1, ![]() ),其焦距为2.
),其焦距为2. 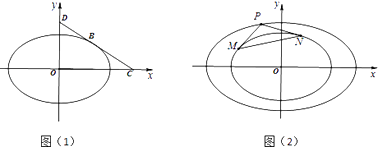
(1)求椭圆C1的方程;
(2)已知椭圆具有如下性质:若椭圆的方程为 ![]() +
+ ![]() =1(a>b>0),则椭圆在其上一点A(x0 , y0)处的切线方程为
=1(a>b>0),则椭圆在其上一点A(x0 , y0)处的切线方程为 ![]() +
+ ![]() =1,试运用该性质解决以下问题:
=1,试运用该性质解决以下问题:
(i)如图(1),点B为C1在第一象限中的任意一点,过B作C1的切线l,l分别与x轴和y轴的正半轴交于C,D两点,求△OCD面积的最小值;
(ii)如图(2),过椭圆C2: ![]() +
+ ![]() =1上任意一点P作C1的两条切线PM和PN,切点分别为M,N.当点P在椭圆C2上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.
=1上任意一点P作C1的两条切线PM和PN,切点分别为M,N.当点P在椭圆C2上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的不恒为零的函数,且对于任意实数x,y满足:f(2)=2,f(xy)=xf(y)+yf(x),an= ![]() (n∈N*),bn=
(n∈N*),bn= ![]() (n∈N*),考查下列结论:
(n∈N*),考查下列结论:
①f(1)=1;②f(x)为奇函数;③数列{an}为等差数列;④数列{bn}为等比数列.
以上命题正确的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某蔬菜商店买进的土豆![]() (吨)与出售天数
(吨)与出售天数![]() (天)之间的关系如下表所示:
(天)之间的关系如下表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(1)请根据上表数据在所给网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (其中
(其中![]() 保留2位有效数字);
保留2位有效数字);
(3)根据(2)中的计算结果,若该蔬菜商店买进土豆40吨,则预计可以销售多少天(计算结果保留整数)?
附:  ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的首项为8,Sn是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为( )
A.S1
B.S2
C.S3
D.S4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com