
ЁОЬтФПЁПЮЊКыбяЁАжаЛЊгХауДЋЭГЮФЛЏЁБЃЌФГжабЇдкаЃФкЖдШЋЬхбЇЩњНјааСЫвЛДЮМьВтЃЌЙцЖЈЗжЪ§![]() ЗжЮЊгХауЃЌЮЊСЫНтбЇЩњЕФВтЪдЧщПіЃЌЯжДг2000УћбЇЩњжаЫцЛњГщШЁ100УћбЇЩњНјааЗжЮіЃЌАДГЩМЈЗжзщЃЌЕУЕНШчЯТЦЕЪ§ЗжВМБэЁЃ
ЗжЮЊгХауЃЌЮЊСЫНтбЇЩњЕФВтЪдЧщПіЃЌЯжДг2000УћбЇЩњжаЫцЛњГщШЁ100УћбЇЩњНјааЗжЮіЃЌАДГЩМЈЗжзщЃЌЕУЕНШчЯТЦЕЪ§ЗжВМБэЁЃ
ЗжЪ§ | [50ЃЌ60ЃЉ | [60ЃЌ70ЃЉ | [70ЃЌ80ЃЉ | [80ЃЌ90ЃЉ | [90ЃЌ100] |
ЦЕЪ§ | 5 | 35 | 30 | 20 | 10 |

ЃЈ1ЃЉдкЭМжазїГіетаЉЪ§ОнЕФЦЕТЪЗжВМжБЗНЭМЃЛ
ЃЈ2ЃЉЙРМЦетДЮВтЪдЕФЦНОљЗжЃЛ
ЃЈ3ЃЉЙРМЦетДЮВтЪдГЩМЈЕФжаЮЛЪ§ЁЃ
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉ74.5ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнБэИёЪ§ОнЃЌРћгУИХТЪЙЋЪНПЩЧѓЕУЗжВМдкЯргІЧјМфФкЕФЦЕТЪЃЌДгЖјПЩвдзїГіЦЕТЪЗжВМжБЗНЭМЃЛ
ЃЈ2ЃЉРћгУУПИіОиаЮЕФЕзБпЕФжаЕуКсзјБъгыЖдгІЕФаЁОиаЮЕФУцЛ§ЕФГЫЛ§ЃЌШЛКѓзїКЭЃЌМДПЩЙРМЦетДЮПМЪдЕФЦНОљЗжЃЛ
ЃЈ3ЃЉгЩжБЗНЭМПЩжЊЃЌжаЮЛЪ§зѓБпКЭгвБпЕФУцЛ§ЯрЕШЃЌОљЮЊ![]() ЃЌРћгУЖдгІЕФЙиЯЕЧѓЕУНсЙћ.
ЃЌРћгУЖдгІЕФЙиЯЕЧѓЕУНсЙћ.
ЃЈ1ЃЉШчЭМЫљЪО
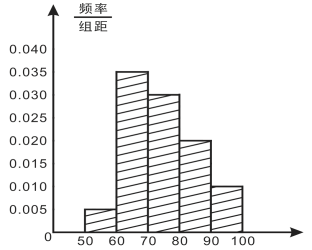
ЃЈ2ЃЉ55ЁС0.005ЁС10+65ЁС0.035ЁС10+75ЁС0.030ЁС10+85ЁС0.020ЁС10+95ЁС0.010ЁС10
ЃН2.75+22.75+22.5+17+9.5
ЃН74.5
ЙРМЦетДЮВтЪдЕФЦНОљЗжЮЊ74.5ЗжЁЃ
ЃЈ3ЃЉгЩжБЗНЭМПЩжЊЃЌжаЮЛЪ§зѓБпКЭгвБпЕФУцЛ§ЯрЕШЃЌОљЮЊ![]() ЃЌЩшжаЮЛЪ§дк70ЁЊ80жЎМфЕФПэЖШЮЊ
ЃЌЩшжаЮЛЪ§дк70ЁЊ80жЎМфЕФПэЖШЮЊ![]() ЃЌдђга
ЃЌдђга
0.005ЁС10+0.035ЁС10+0.030![]() ЃН0.5
ЃН0.5
0.4+0.03![]() ЃН0.5
ЃН0.5
![]() ЃН0.1ЁС
ЃН0.1ЁС![]()
![]() ЃН
ЃН![]()
![]()
![]() ЙРМЦетДЮВтЪдЕФжаЮЛЪ§ЮЊ
ЙРМЦетДЮВтЪдЕФжаЮЛЪ§ЮЊ![]() ЁЃ
ЁЃ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГМИКЮЬхЕФе§ЪгЭМгыВрЪгЭМЖМЪЧБпГЄЮЊ1ЕФе§ЗНаЮЃЌЧвЬхЛ§ЮЊ ![]() ЃЎдђИУМИКЮЬхЕФИЉЪгЭМПЩвдЪЧЃЈ ЃЉ
ЃЎдђИУМИКЮЬхЕФИЉЪгЭМПЩвдЪЧЃЈ ЃЉ 
A.
B.
C.
D.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшOЪЧзјБъдЕуЃЌЭждВCЃКx2+3y2=6ЕФзѓгвНЙЕуЗжБ№ЮЊF1 ЃЌ F2 ЃЌ ЧвPЃЌQЪЧЭждВCЩЯВЛЭЌЕФСНЕуЃЌ ЃЈЂёЃЉШєжБЯпPQЙ§ЭждВCЕФгвНЙЕуF2 ЃЌ ЧвЧуаБНЧЮЊ30ЁуЃЌЧѓжЄЃК|F1P|ЁЂ|PQ|ЁЂ|QF1|ГЩЕШВюЪ§СаЃЛ
ЃЈЂђЃЉШєPЃЌQСНЕуЪЙЕУжБЯпOPЃЌPQЃЌQOЕФаБТЪОљДцдкЃЎЧвГЩЕШБШЪ§СаЃЎЧѓжБЯпPQЕФаБТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЉ.
ЃЉ.
| |||||
|
|
| |||
|
ЃЈ1ЃЉЧыНсКЯЫљИјБэИёЃЌдкЫљИјЕФзјБъЯЕжазїГіКЏЪ§![]() вЛИіжмЦкФкЕФМђЭМЃЛ
вЛИіжмЦкФкЕФМђЭМЃЛ

ЃЈ2ЃЉЧѓКЏЪ§![]() ЕФЕЅЕїЕндіЧјМфЃЛ
ЕФЕЅЕїЕндіЧјМфЃЛ
ЃЈ3ЃЉЧѓ![]() ЕФзюДѓжЕКЭзюаЁжЕМАЯргІ
ЕФзюДѓжЕКЭзюаЁжЕМАЯргІ![]() ЕФШЁжЕ.
ЕФШЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫФИіВЛЭЌЕФКазгРяУцЗХСЫ![]() ИіВЛЭЌЕФЫЎЙћ,ЗжБ№ЪЧНлзгЁЂЯуНЖЁЂЦЯЬбЁЂвдМАЮїЙЯЃЌШУаЁУїЁЂаЁКьЁЂаЁеХЁЂаЁРюЫФИіШЫНјааВТВт
ИіВЛЭЌЕФЫЎЙћ,ЗжБ№ЪЧНлзгЁЂЯуНЖЁЂЦЯЬбЁЂвдМАЮїЙЯЃЌШУаЁУїЁЂаЁКьЁЂаЁеХЁЂаЁРюЫФИіШЫНјааВТВт
аЁУїЫЕЃКЕк![]() ИіКазгРяУцЗХЕФЪЧЯуНЖЃЌЕк
ИіКазгРяУцЗХЕФЪЧЯуНЖЃЌЕк![]() ИіКазгРяУцЗХЕФЪЧЦЯЬбЃЛ
ИіКазгРяУцЗХЕФЪЧЦЯЬбЃЛ
аЁКьЫЕЃКЕк![]() ИіКазгРяУцЗХЕФЪЧЯуНЖЃЌЕк
ИіКазгРяУцЗХЕФЪЧЯуНЖЃЌЕк![]() ИіКазгРяУцЗХЕФЪЧЮїЙЯЃЛ
ИіКазгРяУцЗХЕФЪЧЮїЙЯЃЛ
аЁеХЫЕЃКЕк![]() ИіКазгРяУцОДЕФЪЧЯуНЖЃЌЕк
ИіКазгРяУцОДЕФЪЧЯуНЖЃЌЕк![]() ИіКазгРяУцЗХЕФЪЧЦЯЬбЃЛ
ИіКазгРяУцЗХЕФЪЧЦЯЬбЃЛ
аЁРюЫЕЃКЕк![]() ИіКазгРяУцЗХЕФЪЧНлзгЃЌЕк
ИіКазгРяУцЗХЕФЪЧНлзгЃЌЕк![]() ИіКазгРяУцЗХЕФЪЧЦЯЬбЃЛ
ИіКазгРяУцЗХЕФЪЧЦЯЬбЃЛ
ШчЙћЫЕ:ЁАаЁУїЁЂаЁКьЁЂаЁеХЁЂаЁРюЃЌЖМжЛЫЕЖдСЫвЛАыЁЃЁБдђПЩвдЭЦВтЃЌЕк![]() ИіКазгРязАЕФЪЧЃЈ ЃЉ
ИіКазгРязАЕФЪЧЃЈ ЃЉ
A. ЮїЙЯ B. ЯуНЖ C. ЦЯЬб D. Нлзг
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊfЃЈnЃЉ=1+ ![]() +
+ ![]() +Ё+
+Ё+ ![]() ЃЈnЁЪN*ЃЉЃЌМЦЫуЕУfЃЈ2ЃЉ=
ЃЈnЁЪN*ЃЉЃЌМЦЫуЕУfЃЈ2ЃЉ= ![]() ЃЌfЃЈ4ЃЉЃО2ЃЌfЃЈ8ЃЉЃО
ЃЌfЃЈ4ЃЉЃО2ЃЌfЃЈ8ЃЉЃО ![]() ЃЌfЃЈ16ЃЉЃО3ЃЌfЃЈ32ЃЉЃО
ЃЌfЃЈ16ЃЉЃО3ЃЌfЃЈ32ЃЉЃО ![]() ЃЌгЩДЫЭЦЫуЃКЕБnЁн2ЪБЃЌгаЃЈ ЃЉ
ЃЌгЩДЫЭЦЫуЃКЕБnЁн2ЪБЃЌгаЃЈ ЃЉ
A.fЃЈ2nЃЉЃО ![]() ЃЈnЁЪN*ЃЉ
ЃЈnЁЪN*ЃЉ
B.fЃЈ2nЃЉЃО ![]() ЃЈnЁЪN*ЃЉ
ЃЈnЁЪN*ЃЉ
C.fЃЈ2nЃЉЃО ![]() ЃЈnЁЪN*ЃЉ
ЃЈnЁЪN*ЃЉ
D.fЃЈ2nЃЉЃО ![]() ЃЈnЁЪN*ЃЉ
ЃЈnЁЪN*ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖ![]() ЕФЕзУцЪЧе§ЗНаЮЃЌ
ЕФЕзУцЪЧе§ЗНаЮЃЌ![]() ЕзУцABCDЃЌЕуEдкРтPBЩЯЃЎ
ЕзУцABCDЃЌЕуEдкРтPBЩЯЃЎ
![]() ЧѓжЄЃКЦНУц
ЧѓжЄЃКЦНУц![]() ЦНУцPDBЃЛ
ЦНУцPDBЃЛ
![]() ЕБ
ЕБ![]() ЃЌЧвEЮЊPBЕФжаЕуЪБЃЌЧѓAEгыЦНУцPDBЫљГЩЕФНЧЕФДѓаЁЃЎ
ЃЌЧвEЮЊPBЕФжаЕуЪБЃЌЧѓAEгыЦНУцPDBЫљГЩЕФНЧЕФДѓаЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЪЧЖЈвхдк
ЪЧЖЈвхдк![]() ЩЯЕФЦцКЏЪ§ЃЌЧв
ЩЯЕФЦцКЏЪ§ЃЌЧв![]() ЃЌШєЖдШЮвтЕФmЃЌ
ЃЌШєЖдШЮвтЕФmЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЖМга
ЃЌЖМга![]() ЃЎ
ЃЎ
![]() Шє
Шє![]() ЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
![]() ШєВЛЕШЪН
ШєВЛЕШЪН![]() ЖдШЮвт
ЖдШЮвт![]() КЭ
КЭ![]() ЖМКуГЩСЂЃЌЧѓtЕФШЁжЕЗЖЮЇЃЎ
ЖМКуГЩСЂЃЌЧѓtЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=ax2Љ2bx+aЃЈaЃЌbЁЪRЃЉ
ЃЈ1ЃЉШєaДгМЏКЯ{0ЃЌ1ЃЌ2ЃЌ3}жаШЮШЁвЛИідЊЫиЃЌbДгМЏКЯ{0ЃЌ1ЃЌ2ЃЌ3}жаШЮШЁвЛИідЊЫиЃЌЧѓЗНГЬfЃЈxЃЉ=0ЧЁгаСНИіВЛЯрЕШЪЕИљЕФИХТЪЃЛ
ЃЈ2ЃЉШєbДгЧјМф[0ЃЌ2]жаШЮШЁвЛИіЪ§ЃЌaДгЧјМф[0ЃЌ3]жаШЮШЁвЛИіЪ§ЃЌЧѓЗНГЬfЃЈxЃЉ=0УЛгаЪЕИљЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com