

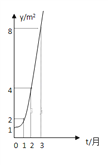
【题目】如图所示的是某池塘中的浮萍蔓延的面积![]() 与时间
与时间![]() 月)的关系
月)的关系![]() 有以下叙述:
有以下叙述:
①这个指数函数的底数是2;
②第5个月时,浮萍的面积就会超过![]()
③浮萍从![]() 蔓延到
蔓延到![]() 需要经过1.5个月;
需要经过1.5个月;
④浮萍每个月增加的面积都相等;
⑤若浮萍蔓延到![]() 所经过的时间分别为
所经过的时间分别为![]() 则
则![]() .其中正确的是
.其中正确的是
A. ①② B. ①②③④ C. ②③④⑤ D. ①②⑤
【答案】D
【解析】由函数图象可知,该函数过点(1,2),所以a=2,则![]() ,故①正确;当t=5时,y=32>30,故②正确;当t=2时,y=4,当
,故①正确;当t=5时,y=32>30,故②正确;当t=2时,y=4,当![]() 时,t=log212,因为log212-2-1.5>0,所以浮萍从
时,t=log212,因为log212-2-1.5>0,所以浮萍从![]() 蔓延到
蔓延到![]() 需要经过的时间超过1.5个月,故③错误;第一个月增加1,第二个月增加2,第三个月增加4,因此④错误;浮萍蔓延到
需要经过的时间超过1.5个月,故③错误;第一个月增加1,第二个月增加2,第三个月增加4,因此④错误;浮萍蔓延到![]() 所经过的时间分别为
所经过的时间分别为![]() ,则
,则![]() ,即
,即![]() ,所以
,所以![]() ,故⑤正确.因此正确的是①②⑤.
,故⑤正确.因此正确的是①②⑤.
点晴:本题考查的是函数模型的应用。解决函数模型应用的解答题,要注意以下几点:①读懂实际背景,将实际问题转化为函数模型.②对涉及的相关公式,记忆要准确.③在求解的过程中计算要正确.另外需要熟练掌握求解方程、不等式、函数最值的方法,才能快速正确地求解.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (e是自然对数的底数),h(x)=1﹣x﹣xlnx.
(e是自然对数的底数),h(x)=1﹣x﹣xlnx.
(1)求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求h(x)的单调区间;
(3)设g(x)=xf′(x),其中f′(x)为f(x)的导函数,证明:对任意x>0,g(x)<1+e﹣2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥P﹣ABCD中,∠ABC=60°,PA=AC=a,PB=PD= ![]() ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1. 
(Ⅰ)证明PA⊥平面ABCD;
(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小;
(Ⅲ)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为 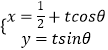 ,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A,B两点,当θ变化时,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游乐园的摩天轮最高点距离地面108米,直径长是98米,均速旋转一圈需要18分钟.如果某人从摩天轮的最低点![]() 处登上摩天轮并开始计时,那么:
处登上摩天轮并开始计时,那么:
(1)当此人第四次距离地面![]() 米时用了多少分钟?
米时用了多少分钟?
(2)当此人距离地面不低于![]() 米时可以看到游乐园的全貌,求摩天轮旋转一圈中有多少分钟可以看到游乐园的全貌?
米时可以看到游乐园的全貌,求摩天轮旋转一圈中有多少分钟可以看到游乐园的全貌?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣ ![]() x2﹣x+a,a∈R
x2﹣x+a,a∈R
(1)当a=0时,求函数f(x)的极值;
(2)若函数f(x)在其定义域内有两个不同的极值点(极值点是指函数取极值时对应的自变量的值),记为x1 , x2 , 且x1<x2 . (ⅰ)求a的取值范围;
(ⅱ)若不等式e1+λ<x1x ![]() 恒成立,求正实数λ的取值范围.
恒成立,求正实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在校运动会上,甲、乙、丙三位同学每人均从跳远,跳高,铅球,标枪四个项目中随机选一项参加比赛,假设三人选项目时互不影响,且每人选每一个项目时都是等可能的
(1)求仅有两人所选项目相同的概率;
(2)设X为甲、乙、丙三位同学中选跳远项目的人数,求X的分布列和数学期望E(X)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com