
分析 (1)由题可知MP=2,M(0,2),由此可求点P的坐标;
(2)求出四边形PAMB的面积和周长,由勾股定理和过M作MP'垂直于直线时,可得最短距离为d,即有最小值;
(3)利用向量的数量积公式,计算$\overrightarrow{PA}$•$\overrightarrow{PB}$,结合切线长公式,利用配方法,即可求得最小值.
解答 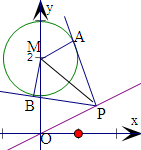 解:(1)设P(2m,m),
解:(1)设P(2m,m),
由题可知MP=2,M(0,2),
所以(2m)2+(m-2)2=4,
解之得m=0或m=$\frac{4}{5}$.
故所求点P的坐标为P(0,0)或($\frac{8}{5}$,$\frac{4}{5}$);
(2)四边形PAMB的面积为S=$\frac{1}{2}$PA•AM+$\frac{1}{2}$PB•BM=PA,
PA2=PM2-1,当PM最小时,PA最小.
过M作MP'垂直于直线时,最短距离为d=$\frac{|0-2×2|}{\sqrt{5}}$=$\frac{4}{\sqrt{5}}$,
即有面积最小为P'A=$\frac{\sqrt{55}}{5}$;
周长为PA+PB+AM+BM=2PA+2,
即有周长的最小值为2+$\frac{2\sqrt{55}}{5}$;
(3)设P(2m,m),则$\overrightarrow{PA}$•$\overrightarrow{PB}$=|$\overrightarrow{PA}$|2cos∠APB,
又|$\overrightarrow{PA}$|2=PM2-1,cos∠APB=1-$\frac{2}{P{M}^{2}}$,
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$=PM2+$\frac{2}{P{M}^{2}}$-3
又PM2=(2m)2+(m-2)2=5m2-4m+4∈[$\frac{16}{5}$,+∞),
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$=(PM-$\frac{\sqrt{2}}{PM}$)2+2$\sqrt{2}$-3∈[$\frac{33}{40}$,+∞),
故$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值为$\frac{33}{40}$.
点评 本题考查直线与圆的位置关系,考查向量的数量积公式,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (1,0) | C. | (0,-1) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\sqrt{7}$) | B. | (-$\sqrt{7}$,$\sqrt{7}$) | C. | ($\sqrt{7}$,+∞) | D. | ($-∞,-\sqrt{7}$)$∪(\sqrt{7,}+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com