【题目】如图，在几何体
中，四边形
为矩形，
且
，
为
的中点．
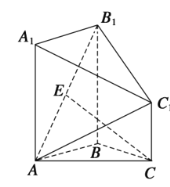
（1）求证：
平面
；
（2）若平面
平面
，
，
，求三棱锥
的体积．
【答案】（1）证明见解析（2）
【解析】
（1）取A1B1中点F，连接EF，FC1， 证明CE∥C1F，即可证明线面平行；
（2）根据三棱锥的等积法得
，即可求得答案.
(1)证明 如图，取A1B1中点F，连接EF，FC1，
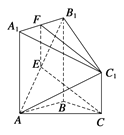
∵E为AB1中点，∴EF//A1A且EF=
A1A，
∵AA1∥CC1且AA1=2CC1，
∴EF//CC1且EF=CC1，即四边形EFC1C为平行四边形，
∴CE∥C1F.
∵
，
，
∴CE∥平面A1B1C1.
(2) ∵平面AB B1A1⊥平面ABC，交线为AB
又矩形AB B1A1中A A1⊥AB，∴AA1⊥平面ABC，
∵AA1∥CC1，∴CC1⊥平面ABC，
∵BB1∥CC1，
，
，
∴BB1∥
，
∴
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】如图,在四棱锥
中, 平面
平面
,
.
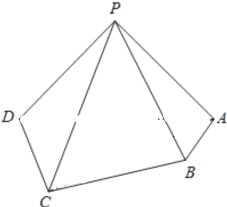
（1）求证:
平面
；
（2）求直线
与平面
所成角的正弦值；
（3）在棱
上是否存在点
,使得
平面？若存在, 求
的值；若不存在, 说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2016年1月14日，国防科工局宣布，嫦娥四号任务已经通过了探月工程重大专项领导小组审议通过，正式开始实施.如图所示，假设“嫦娥四号”卫星将沿地月转移轨道飞向月球后，在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行.若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴长，给出下列式子：
①a1＋c1＝a2＋c2； ②a1－c1＝a2－c2； ③c1a2>a1c2. ④
其中正确式子的序号是（ ）
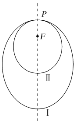
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的离心率
，且圆
过椭圆的上，下顶点.
（1）求椭圆的方程.
（2）若直线
的斜率为
，且直线交椭圆于
、
两点，点关于点的对称点为
，点
是椭圆上一点，判断直线
与
的斜率之和是否为定值，如果是，请求出此定值：如果不是，请说明理.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
（
、
为实常数）.
（1）当
时，证明：
不是奇函数；
（2）设是奇函数，求与的值；
（3）当是奇函数时，研究是否存在这样的实数集的子集
，对任何属于的
、
，都有
成立？若存在试找出所有这样的；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知二次函数
的值域为
.
（1）判断此函数的奇偶性，并说明理由；
（2）判断此函数
在的单调性，并用单调性的定义证明你的结论；
（3）求出
在
上的最小值
，并求的值域.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，以O为极点，x轴非负半轴为极轴建立极坐标系圆C的极坐标方程为
，直线
的参数方程为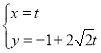
（t为参数），直线和圆C交于A，B两点，P是圆C上不同于A，B的任意一点.
（1）求圆C及直线的直角坐标方程；
（2）求
面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】众所周知的“太极图”，其形状如对称的阴阳两鱼互抱在一起，因而也被称为“阴阳鱼太极图”．如图是放在平面直角坐标系中的“太极图”，整个图形是一个圆形，其中黑色阴影区域在y轴右侧部分的边界为一个半圆．给出以下命题：
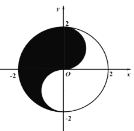
①在太极图中随机取一点，此点取自黑色阴影部分的概率是
；
②当
时，直线
与黑色阴影部分有公共点；
③黑色阴影部分中一点
,则
的最大值为2．
其中所有正确结论的序号是（ ）
A.①B.②C.①③D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
